Графы и деревья

Такая структура, как граф (в качестве синонима используется также термин «cеть»), имеет самые различные применения в информатике и в смежных приклад­ных областях, поэтому познакомимся с основными понятиями теории графов.

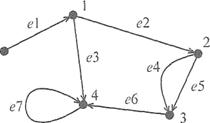
Граф G = (V, Е) задается парой конечных множеств V и Е. Элементы первого множества v1, v2,..., vM называются вершинами графа (при графическом представлении им соответствуют точки). Элементы второго множества el, e2,..., eN называют ребрами. Каждое ребро определяется парой вершин (при графическом представлении ребро соединяет две вершины графа). Если ребра графа определяются упорядоченными парами вершин, то такой граф называют ориентированным (на чертеже при изображении ориентированного графа на каждом ребре ставят стрелку, указы­вающую его направление). Ориентированный граф с пятью вершинами и семью ребрами изображен на рисунке 1.6.

Рисунок 1.6. - Пример ориентированного графа

Если две вершины соединены двумя или более ребрами, то эти ребра называют параллельными (например, ребра е4 и е5). Если начало и конец ребра совпадают, то такое ребро называется петлей (например, ребро e7). Граф без петель и параллельных ребер называется простым.

Если ребро ек определяется вершинами vi и vj (будем обозначать этот факт следующим образом: ек = (vi, vj), то говорят, что ребро ек инцидентно вершинам vi, vj. Две вершины vi и vj называются смежными, если в графе существует ребро vi, vj).

Последовательность вершин vi1, vi2,..., vik, таких, что каждая пара (vi(j-1), vij) при 1 <j≤ к определяет ребро, называется маршрутом в графе G. Вершины vil и vik _называют концевыми вершинами маршрута, все остальные входящие в него вершины - внутренними. Маршрут, в котором все определяемые им ребра различны, называют цепью. Цепь считаютзамкнутой, если ее концевые вершины совпадают. Замкнутая цепь, в которой все вершины (за исключением концевых) различны, называется циклом. Незамкнутая цепь, в которой все вершины различны, носит название путь. Если в ориентированном графе существует путь из vi в vj, то говорят, что вершина vj достижима из вершины vi.

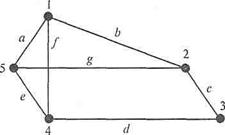
Две вершины vi и vj называют связанными в графе G, если в нем существует путь, для которого эти вершины являются концевыми. Граф G называется связным, если каждые две вершины в нем являются связанными. На рис. 2.2 изображен простой неориентированный связный граф.

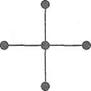
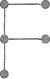
Последовательность вершин v1, v5, v4, v3, например, определяет путь, а последовательность вершин v1, v5, v4, v3, v2, v1 - цикл. Деревом будем называть неориенти­рованный связный граф без циклов. Лес - это любой граф без циклов. На рисунке 1.7 показаны возможные деревья с пятью вершинами.

Рисунок 1.7 - Пример неориентированного связного графа

Рисунок 1.8. - Примеры деревьев

Анализ приведенных здесь понятий и определений показывает, что в качестве моделей графы удобно использовать в тех случаях, когда рассматривается система каких-либо объектов, между которыми существуют определенные связи, отноше­ния, когда изучается структура системы, возможности ее функционирования. В информатике графы используются в разделах: операционные системы, алгорит­мизация, структуры данных, информационное моделирование и др.

Важным вопросом, особенно для приложений теории графов, является определе­ние возможных способов представления графов. Самый простой способ - полное перечисление множеств V и Е. Однако очевидно, что в этом случае выявление у графа различных характеристик и свойств будет крайне затруднительным. Граф можно представить в виде некоторого графического изображения и визуально определить некоторые свойства и характеристики заданного графа. Однако при наличии в графе большого числа ребер и вершин этот способ также мало пригоден.

Рассматривая различные возможные способы представления графов, мы должны иметь в виду потребность ввода соответствующей информации в компьютер. В этой связи ввод информации в числовом виде предпочтителен, хотя современные технические средст­ва допускают ввод и графической информации (таблиц, текста, графиков, рисунков и т.д.), после чего может производиться обработка такой информации.

Контрольные вопросы:

1.Дайте определение множества?

2.Какое бывает множество?

3.Какие виды множества вы знаете?

4.Кто основатель логики?

5.Что такое таблица истинности?

6.Назовите основные законы логики?

7.Что такое граф?

8. Что такое дерево?

Темы рефератов:

1.Функции, отношения и множества.

2.Основы логики.

3.Таблицы истинности

4.Основные законы логики.

5.Неориентированные и ориентированные графы.

6.Деревья.

7. Стратегии обхода графов.

Контрольные задания СРС:

1.Основы дискретной математики.

2. Функции, отношения и множества.

3. Основы логики.

4. Таблицы истинности.

5. Основные законы логики.

6. Неориентированные и ориентированные графы.

7. Деревья.

8. Стратегии обхода графов.

Дата добавления: 2013-12-13