Прочность. Способность детали сопротивляться разрушению – оценивается несколькими способами: мощью допускаемых напряжений; б) запасами в) статистическими запасами

Способность детали сопротивляться разрушению – оценивается несколькими способами: мощью допускаемых напряжений; б) запасами в) статистическими запасами прочности.

Наибольшее распространение получил метод расчета по допускаемым напряжениям, согласно которому наибольшее напряжение σ_шах в некоторой точке нагруженной детали не должно превышать определенной величины, свойственной дан­ному материалу и типу детали.

Условие прочности детали по допускаемому напряжению имеет вид

σ_max ≤ [σ] (16.1)

где [σ] - допускаемое напряжение.

Такая оценка удобна, и поэтому на практике для одно­типных конструктивных элементов (деталей), устоявшейся тех­нологии их изготовления, стабильных условий нагружения разработана система допускаемых напряжений, обобщающая предшествующий опыт эксплуатации машин, приборов и аппара­тов различного назначения.

Однако такой оценке прочности присущи и недостатки:

1) величина допускаемого напряжения носит условный ха­рактер, так как не отражает характера предполагаемого раз­рушения, режима нагружения и других факторов, влияющих на надежность;

2) допускаемое напряжение, особенно при переменной на­грузке, зависит от геометрии детали, материала, технологии изготовления, что затрудняет его использование в качестве нормативной характеристики;

3) величина [σ] не дает представления о надежности де­тали в явном виде, так как в формуле (16.1) не пока­зано соотношение действующих и предельных напряжений для материала детали (предела текучести σ_т, предела проч­ности σ_в, предела выносливости и др.).

В инженерных расчетах допускаемые напряжения используют в основном для предварительных расчетов, связанных с приб­лиженным определением основных размеров деталей. Широкое распространение получил также расчет по запасам прочности. Условие прочности в этом случае

n = σ_пред / σ_max (16.2)

где n - запас прочности; σ_пред - предельное напряжение (предел прочности при постоянных нагрузках, предел выносливости при переменных нагрузках), полученное экспериментально или взятое из справочника; σ_max — максимальное напряжение в опас­ной точке детали, вычисленное при наибольшей (ожидаемой или установленной тензометрированием) рабочей нагрузке. Величина σ_пред отражает геометрию детали, технологию ее изготовления и условия нагружения, поэтому величина необходимого запаса прочности имеет стабильное значение.

Условия прочности по допускаемым напряжениям и за­пасам прочности связаны соотношением

[σ]= σ_пред / n (16.3)

При действии статических нагрузок иногда используют запас прочности по несущей способности

n = F_разр / F (16.4)

показывающий отношение нагрузок в момент разрушения и в рабочих условиях.

В описанных методах оценки прочности носят детермини­рованный характер и не учитывают должным образом неизбеж­ное рассеяние разрушающих и максимальных напряжений.

Статистические запасы прочности являются более обосно­ванными характеристиками прочностной надежности, в осо­бенности для отказов конструкций с тяжелыми последстви­ями.

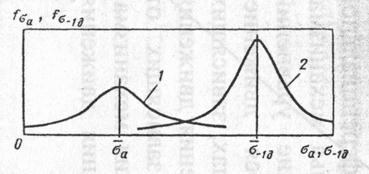
Рис. 16.1. Кривые плотности распределения переменных на­пряжений и пределов выносли­вости

На рис. 16.1 в качестве примера показаны кривые плот­ности распределения переменных напряжений σ_a наиболее нагруженной точке детали (кривая 1) и пределов выносливости детали σ_-1д (кривая 2). Переменные напряжения в детали в процессе работы определяют с помощью тензометрирования. Рассеяние рабочих напряжений вызвано колебаниями нагрузки при работе машины.

Предел выносливости детали определяют экспериментально на некоторой базе испытаний (обычно 10⁷ циклов). Разброс характеристик сопротивления усталости деталей обусловлен нестабильностью механических свойств металла даже в пре­делах одной плавки, отклонениями в режиме термообработки, отклонениями размеров деталей в пределах допусков, ми­кроскопическими источниками рассеяния, связанными с не­однородной структурой материала и др.

Так как разрушающее и действующее -напряжения явля­ются случайными величинами, то и запас прочности конкретной детали является случайной величиной с функцией распределения Р(п):

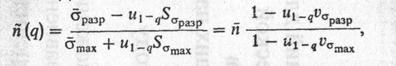
где u_1-q — односторонний квантиль доверительной вероятности Р_д = 1 – q;

n = σ_разр / σ_mах - запас прочности по средним на­пряжениям;

υ_σразр = S _σразр / σ_разр и υ_σmax = S _σmax / σ_max - коэффи­циенты вариации.

Величины u_1-q для некоторых значений уровня значимости следующие:

q	0,10	0,05	0,01	0,0014
u1-q	1,29	1,64	2,33	3,0

Статистические запасы прочности, как и обычные запасы прочности, имеют условное значение. Их используют как критерии сравнения надежности вновь создаваемых изделий с изделиями, удовлетворительно эксплуатируемыми.

Основное преимущество статистических запасов прочности перед детерминистскими (обычными) запасами состоит в том, что сопоставление приводится к одинаковым условиям по рассеянию значений σ_разр и σ_mах (по объему используемой информации).

Выпол­нение требований прочности при статическом, циклическом и ударном нагружениях должно исключить возможность раз­рушения, а также возникновения недопустимых остаточных и упругих деформаций.

Дата добавления: 2013-12-13