Исследование устойчивости по линейному приближению

В некоторых случаях устойчивость состояния равновесия нелинейной системы можно исследовать по уравнениям первого приближения, полученным в результате линеаризации уравнений состояния в малой окрестности точки равновесия. Данный способ был предложен A.M. Ляпуновым.

Рассмотрим этот подход для нелинейной автономной стационарной системы

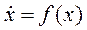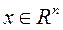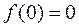, , . (7)

Разложим f(x) в ряд Тейлора в малой окрестности состояния равновесия:

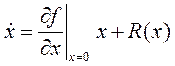, (8)

где R (x) - члены ряда разложения выше первой степени; матрица частных производных 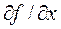имеет вид

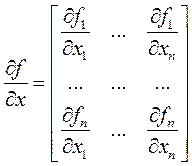. (9)

Отбрасывая члены ряда разложения R (x), вместо (8) получим

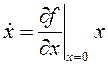. (10)

Матрица частных производных (9) рассматривается в точке равновесия, поэтому представляет собой числовую матрицу коэффициентов (якобиан), для которой введем обозначение

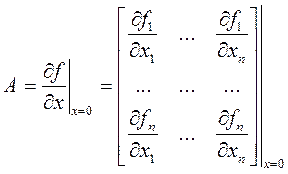. (11)

С учетом (11) окончательно уравнение первого приближения системы (10) принимает вид

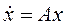, (12),

т. е. соответствует описанию линейной автономной системы.

Согласно теореме, доказанной A.M. Ляпуновым, устойчивость исходной системы (7) связана с устойчивостью линеаризованной системы (12).

Теорема.

· Если линеаризованная система устойчива, то исходная нелинейная система будет асимптотически устойчивой «в малом» относительно исследуемого состояния равновесия.

· При неустойчивой линеаризованной системе процессы в исходной нелинейной системе будут также неустойчивыми.

· Если линеаризованная система находится на границе устойчивости (корни нулевые или мнимые), то об устойчивости нелинейной системы ничего нельзя сказать. Это критический случай, и нужны дополнительные исследования для окончательного суждения об устойчивости нелинейной системы (7), которую определяют члены высшего порядка ряда разложения R (x).

Пример 1.

По линейному приближению оценить устойчивость относительно одного из положений равновесия системы, математическая модель которой имеет вид

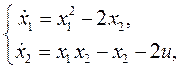u= 0.

Запишем уравнения равновесия системы

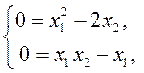
откуда определим одну из точек равновесия: 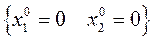. В ее малой окрестности линеаризуем исходную систему

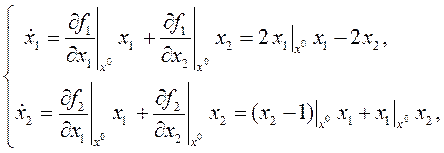
которая примет вид

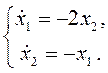
Матрица линеаризованной системы следующая:

.

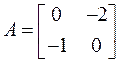Запишем для нее характеристическое уравнение

.

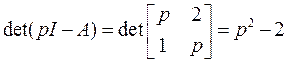Как видим, линеаризованная система неустойчива, следовательно, исходная система также неустойчива.

Дата добавления: 2014-01-04