Потеря устойчивости плоской фермы изгиба тонкой полосы и двутавровой балки

Если тонкая и высокая балка прямоугольного сечения изгибается в главной плоскости с наибольшей жесткостью, то плоская форма изгиба за критическими нагрузками становится неустойчивой и происходит выпучивание балки.

Рассмотрим тонкую высокую балку, загруженную посредине пролета силой Р

а) в) y y₁

Z U

P

Z h M_1(X)

M_X V

d b

l/2 l/2 x₁

b

б)

P

В самый начальный момент потери устойчивости некоторое сечение на расстоянии Z от левой опоры повернулось на малый угол b, т.е. его новая ось у₁ наклонена к вертикали под этим углом. Горизонтальное смещение средней линии сечения = U, вертикальное = V.

Т.е. в момент потери устойчивости, наряду с вертикальным изгибом, появляется изгиб балки в боковом направлении, а также ее кручение.

Определим дополнительную потенциальную энергию накапливаемую полосой в момент потери устойчивости, учитывая боковой изгиб и кручение полосы.

Момент, изгибающий полосу в боковом направлении

учитывая, что угол b бесконечно мал sin b = b

Потенциальная энергия, накапливаемая в результате бокового изгиба

,

где J_у - момент инерции сечения относительно оси У.

Учитывая, что сила приложена посредине длины балки, возьмем интеграл на половине ее длины и результат удвоим

(30)

Определим потенциальную энергию, накапливаемую в полосе за счет ее кручения

,

или

,

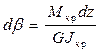отсюда

.

Потенциальная энергия в элементе бесконечно малой длины

,

.

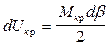Умножим это выражение и разделим на dz

.

Потенциальная энергия в полосе кручения

или

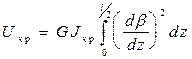(31)

Полная потенциальная энергия внутренних сил, накапливаемая полосой после потери устойчивости

(32)

Определим работу внешних сил в момент потери устойчивости полосой

P

Ввиду малости перемещений, работа внешних

P d сил при повороте сечения = 0

Работа Р на перемещении d равна

А = Р×d,

без коэффициента 1/2 т.к. в момент потери устойчивости сила имеет свою постоянную величину.

Перемещение d определим оп интегралу Мора:

,

где М_у - момент, вызывающий боковой изгиб силой Р: ;

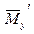- то же единичной силой: .

Тогда:

или:

(33)

Приравнивая потенциальную энергию внутренних сил работе внешних сил:

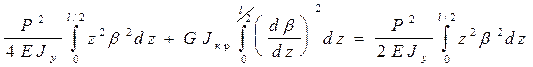
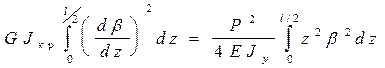
или

(34)

Задаемся выражением для углов закручивания сечений, удовлетворяющих граничным условиям задачи:

, ;

1) при z = 0 b = 0

2) при z = l b = 0

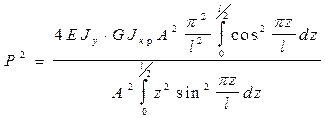
Вычислив интегралы:

(35)

Точное решение

Для двутаврового сечения:

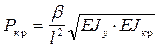(36)

где b - коэффициент, определяемый по таблицам справочников.

Дата добавления: 2014-01-04