Обобщенные многочлены наилучших среднеквадратических приближений

НАИЛУЧШИЕ СРЕДНЕКВАДРАТИЧНЫЕ ПРИБЛИЖЕНИЯ.

Лекция 19.

Вернемся к общей постановке задачи аппроксимации функций.

Пусть аппроксимируемая функция f (x) и аппроксимирующая функция j(x) непрерывны на отрезке [ а, b ], и аппроксимация должна производиться так, чтобы функция j(x) «в среднем хорошо описывала» поведение функции f (x) при х Î [ а, b ]. Будем здесь постоянно иметь в виду две аппроксимационные ситуации: первая, это когда функция f (x) считается (по крайней мере, теоретически) известной в любой точке х отрезка С [ а, b ], и близость между f (x) и j(x) понимается в интегральном смысле, и вторая, когда f (x) известна (причем приближенно) только в п + 1 точках х ₀, х ₁ ,..., х_n отрезка [ а, b ], в которых и производится согласование f (x) с j(x) подобно тому, как это делалось в предыдущем параграфе. В связи с этим, будем параллельно рассматривать:

а) пространство С_L [ а, b ] непрерывных на [ а, b ] функций со скалярным произведением

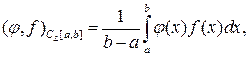(19.1)

и нормой

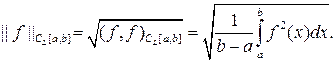
б) пространство R _{n +1}[ а, b ] сеточных функций, определенных в точках х_i Î [ а, b ] (i = 0,1,.... n), со скалярным произведением

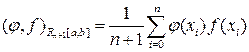(19.2)

и нормой

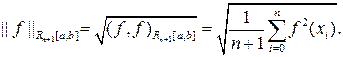
Введенные нормы характеризуют близость функций f (x) и j(x) в пространствах С_L [ а, b ] и R _{n +1}[ а, b ] через малость выражени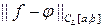й или 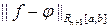соответственно; по отношению к приближенному равенству f (x)» j(x) при х Î [ а, b ] они представляют собой интегральную и точечную (дискретную) среднеквадратические ошибки.

В силу того, что

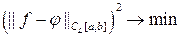и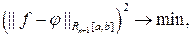

можно сказать, что применение метода наименьших квадратов к аппроксимации функции f (x) функцией j(x) заданного семейства означает подбор такой функции j(x), которая минимизирует среднеквадратическую погрешность приближенного равенства f (x)» j(x) в интегральном или в точечном смысле; в связи с этим, она называется наилучшим среднеквадратическим приближением f (x) на заданном семействе функций.

Рассмотрим, к чему сводится процесс построения наилучших среднеквадратических приближений в одном конкретном, но достаточно общем случае, когда аппроксимирующая f (x) функция j(x) представляет собой линейную комбинацию нескольких других, вообще говоря, более простых (базисных) функций.

Пусть 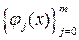— некоторая заданная на [ а, b ] система линейно независимых функций. Обобщенным многочленом будем называть функцию

Q_m (x) ^:= с ₀j₀(x) + с ₁j₁(x) +... + с_т j₁(x) (19.3)

где с ₀, с ₁, …, с_т — произвольные вещественные числа (коэффициенты обобщенного многочлена). Поскольку функции 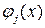считаются заданными, построение обобщенного многочлена наилучшего среднеквадратического приближения для данной функции f (x) сводится к нахождению оптимального набора 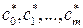коэффициентов Q_m (x) в (19.3) на основе метода наименьших квадратов, т.е. к решению задач минимизации:

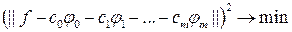
После элементарных преобразований она может быть переписана в терминах скалярных произведений (см. (19.1) и (19.2)):

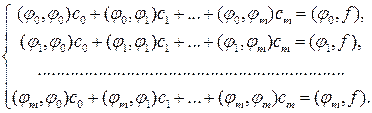(19.4)

Если функции 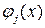образуют систему линейно независимых элементов пространства, то полученная симметричная линейная алгебраическая система, называемая нормальной системой МНК, имеет заведомо отличный от нуля определитель (это известный определитель Грамма, и значит, однозначно разрешима. Следовательно, при заданном базисе 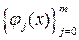путем решения системы (19.4) можно найти единственный обобщенный многочлен

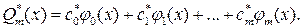
Анализируя СЛАУ (19.4), приходим к выводу, что она чрезвычайно упрощается в случае, когда базисные функции 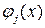образуют на [ а, b ] ортогональную систему.

Как известно, взаимная ортогональность функций из множества 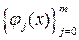означает, что (j _j, j _k)= 0 при любых k ¹ j. Следовательно, коэффициенты с ₀, с ₁, …, с_т обобщенного многочлена наилучшего среднеквадратического приближения (19.3) могут быть сразу выписаны из системы (19.4), превратившейся в диагональную, а именно:

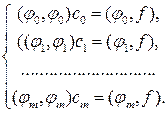(19.5)

В таком случае найденные коэффициенты называются коэффициентами Фурье, а обобщенный многочлен (19.3) с этим оптимальным набором коэффициентов (т.е. обобщенный многочлен наилучшего среднеквадратического приближения для f (x) называется обобщенным многочленом Фурье.

Еще проще построение таких многочленов, когда система 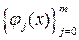— ортонормированная. Тогда ||j _j || = 1, и из (19.5) следует, что c_j = (j _j, f) при любом j Î {0,1,..., m }, т.е. аппроксимация функции f (x) обобщенным многочленом Фурье имеет вид

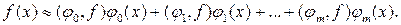(19.6)

В частности, в математическом анализе достаточно подробно изучаются представления функций (не обязательно непрерывных) выражениями типа (19.6), в которых в качестве базисных функций используются функции ортогональной на [ -p, p] системы {sin kx, cos kx | k Î N₀}. Такие представления в этом случае называются отрезками тригонометрических рядов Фурье.

Дата добавления: 2014-01-04