Свойства соленоидального поля

Соленоидальное поле

Поле называют соленоидальным, если оно является полем ротора некоторой векторной функции , т.е. 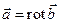; при этом вектор называют векторным потенциалом поля .

1). Поле является соленоидальным тогда и только тогда, когда .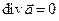

2). В соленоидальном поле поток через замкнутую поверхность, не содержащую внутри особых точек поля, равен нулю.

3). В соленоидальном поле потоки через замкнутые поверхности, окружающие все особые точки поля, равны между собой.

4). В соленоидальном поле поток через любое поперечное сечение векторной трубки сохраняет постоянное значение (называемое интенсивностью трубки).

Проверим эти свойства.

1). Пусть поле ─ соленоидально, т.е.

;

тогда

можно показать, что справедливо и обратное: если 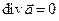, то .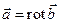

2). В соленоидальном поле 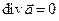и потому по формуле Остроградского поток через замкнутую поверхность, не содержащую внутри особых точек поля,

.

3). Пусть 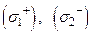─ поверхности, окружающие все особые точки поля; их ориентация указана на рис. 78. Обозначим через 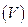─ тело с границей ; внутри тела 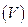поле определено, 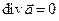, и потому по формуле Остроградского

.

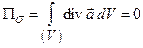С другой стороны, 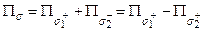и следовательно,.

Рис. 79

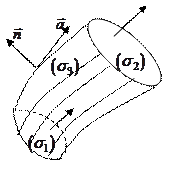4). Рассмотрим векторную трубку поля, т.е. совокупность его векторных линий, пересекающих некоторую замкнутую линию (рис. 79). Пусть поперечные сечения векторной трубки с указанной на рис. 79 ориентацией; поверхность векторной трубки, состоящая из векторных линий; граница тела .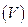

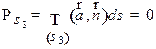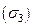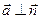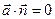Вычислим поток поля через поверхность : с одной стороны, по свойству 2) этот поток равен нулю; с другой стороны, , а , т.к. состоит из векторных линий, значит, вектор поля направлен по касательной к векторной линии, т.е. и . Следовательно, или .

Пример 12.4. Найти поток поля напряженностей 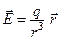, создаваемого зарядом , через произвольную замкнутую поверхность .

Решение. Дивергенция поля равна нулю (пример 10.9), потому поле напряженностей является соленоидальным всюду, где определено (т.е. в точках 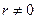, отличных от начала координат).

Тогда по свойству 2) соленоидального поля поток поля через любую замкнутую поверхность, не окружающую начала координат, равен нулю.

По свойству 3) соленоидального поля поток поля через замкнутую поверхность, окружающую начало координат, равен, например, потоку этого поля через сферу с центром в начале координат (он был вычислен в примере 10.1) и равен .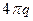

Дата добавления: 2014-01-04