
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Химические свойства нуклеиновых кислот
|
|
|
|
Таблица интегралов.
Запишем таблицу интегралов, вытекающую из основных формул дифференциального исчисления.
| № | 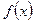
| 
|
| 1. | 
| |
| 2. |  , , 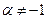
| 
|
| 3. |  , , 
| 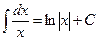
|
| 4. |  , ,  , , 
| 
|

| 
| |
| 5. | 
| 
|

| 
| |
| 6. | 
| 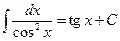
|

|  на интервалах, где подынтегральные функции непрерывны
на интервалах, где подынтегральные функции непрерывны
| |
| 7. |  , , 
| 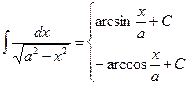
|
| 7a. |  , , 
| 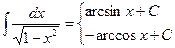
|
| 8. | 
| 
|
| 8a. | 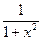
| 
|
| 9. | 
| 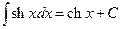
|
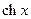
| 
| |
| 10. | 
| 
|
 , , 
| 
| |
| 11. | 
| 
|
 , , 
| 
| |
| 11a. | 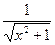
| 
|
| 12. |  , , 
| 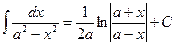
|
| 12a. |  , , 
| 
|
Справедливость приведённых формул проверяется непосредственно дифференцированием (см. определение 21.1). Например, формула (2) верна, так как  равна подынтегральной функции (2).
равна подынтегральной функции (2).
Докажем (3). Пусть  ,
,  , тогда
, тогда  . Если же
. Если же  , то
, то  и
и 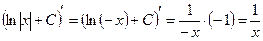 , то есть (3) доказана.
, то есть (3) доказана.
Докажем (11a):
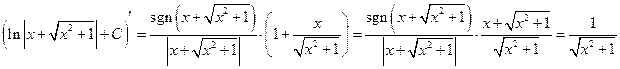 .
.
С другой стороны,  , по теореме 21.2
, по теореме 21.2  . Так как
. Так как 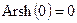 , то
, то  и
и  .
.
Формулы 7, 8, 12 докажем позднее.
Таблицу интегралов необходимо пополнять нетривиальными примерами в процессе изучения методов интегрирования. Применяя свойство 5° неопределённого интеграла, можно написать более сложную таблицу интегралов, включающую, например, 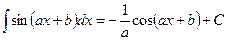 и т.п. интегралы.
и т.п. интегралы.
☼ Замечание 21.1. Операция дифференцирования элементарных функций снова приводит к элементарным функциям, операция интегрирования может привести к неэлементарным функциям, то есть к функциям, которые не выражаются через конечное число арифметических операций и суперпозиций элементарных функций. Например, следующие интегралы не интегрируются в элементарных функциях:
 – интеграл Пуассона[1],
– интеграл Пуассона[1],
 ,
,  – интегралы Френеля[2],
– интегралы Френеля[2],
 – интегральный логарифм,
– интегральный логарифм,
 – интегральный косинус,
– интегральный косинус,
 – интегральный синус.
– интегральный синус.
Указанные интегралы хотя и существуют, но не являются элементарными функциями. Имеются другие способы для их вычисления. Например, интегральный синус можно представить в виде ряда: так как  , то
, то  и
и
 . ☼
. ☼
[1] Пуассон Симеон Дени (1781-1840) – французский математик, механик и физик, один из основоположников математической физики.
[2] Френель Огюстен Жак (1788-1827) – французский физик и математик.
Цепи НК содержат большое количество фосфатных остатков, обладающих высокой кислотностью и ионизированных в водной среде. Поэтому молекулы НК несут на себе большой отрицательный заряд, в выделяемых препаратах НК представляют собой натриевые соли.
Сложноэфирные связи, соединяющие полинуклеотидные цепи, неустойчивы в кислой и щелочной средах, и НК в этих условиях подвергаются гидролизу:

КОМПЛЕМЕНТАРНОСТЬ АЗОТИСТЫХ ОСНОВАНИЙ
Комплементарность – это соответствие формы двух сложных линий, которые подходят друг к другу "как ключ к замку".
Комплементарные пары оснований:

В паре А-Т тимин может быть (при переходе ДНК→РНК) заменен урацилом, и пара становится А-У ("взаимозаменяемость" тимина и урацила).
Биологическое значение комплементарных взаимодействий заключается в том, что обеспечивают точность передачи информации от одной НК к другой.
Вторичная структура ДНК
- представляет собой спираль, состоящую из двух комплементарных друг другу и антипараллельных полинуклеотидных цепей ("двойная спираль"):

Биологическая роль "двойной спирали":
1) Она обеспечивает сохранность генетической информации (ядерный нуклеопротеидный комплекс "ДНК-Гистоны");
2) Обеспечивает восстановление информации при повреждении ДНК (репарация после мутаций).
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 401; Нарушение авторских прав?; Мы поможем в написании вашей работы!