
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Степенные ряды
|
|
|
|
| Опр. | Функциональный ряд вида
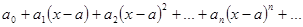 (1)
где (1)
где 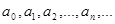 постоянные числа называются степенным рядом, а числа постоянные числа называются степенным рядом, а числа 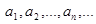 - коэффициентами этого ряда. - коэффициентами этого ряда.
|
В частном случае 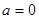 степенной ряд (1) принимает более простой вид
степенной ряд (1) принимает более простой вид
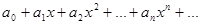 (2)
(2)
Степенной ряд (2) сходится в точке 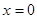 т.к. сумма ряда равна
т.к. сумма ряда равна  . Для выявления же области сходимости ряда и её характерной особенности, докажем теорему Абеля:
. Для выявления же области сходимости ряда и её характерной особенности, докажем теорему Абеля:
| Теорема Абеля | Если степенной ряд (2) сходится при некотором значении аргумента 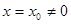 , то он абсолютно сходится при любом значении , то он абсолютно сходится при любом значении 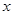 , удовлетворяющем условию , удовлетворяющем условию  . Если же при некотором значении . Если же при некотором значении 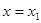 , ряд (2) расходится, то он расходится и при любом , ряд (2) расходится, то он расходится и при любом 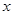 , для которого , для которого  . .
|
Доказательство:
1)Пусть при 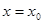 ряд (2) сходится:
ряд (2) сходится:
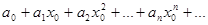 (3)
(3)
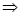 общий член этого ряда
общий член этого ряда 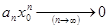 .
. 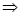 Ч.п.
Ч.п.  - сходится
- сходится 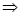 она ограничена, т.е.
она ограничена, т.е.  число
число  , что все члены ряда (3) по абсолютной величине не превосходят числа
, что все члены ряда (3) по абсолютной величине не превосходят числа 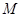 :
:
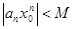 .
.
Перепишем ряд (2) в виде:
 (4)
(4)
и построим ряд из абсолютных величин его членов:
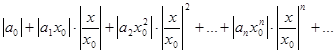 (5)
(5)
а также запишем ряд вида:
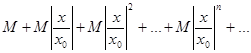 (6)
(6)
Для доказательства первой части теоремы, предположив сходимость ряда (2) в т. 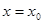 , требуется показать, что этот ряд будет сходится для
, требуется показать, что этот ряд будет сходится для  :
:  .
.
Ряд (6) сходится как ряд геометрической прогрессии со знаменателем  . Тогда ряд (5) сходится по признаку сходимости, т.к. члены этого ряда меньше соответствующих членов ряда (6). Но тогда по достаточному приз0наку сходимости знакопеременного ряда сходится ряд (4) или, что то же самое, ряд (2), причем абсолютно.
. Тогда ряд (5) сходится по признаку сходимости, т.к. члены этого ряда меньше соответствующих членов ряда (6). Но тогда по достаточному приз0наку сходимости знакопеременного ряда сходится ряд (4) или, что то же самое, ряд (2), причем абсолютно.
2)Пусть в некоторой точке 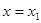 ряд (2) расходится. Предположим противное, что ряд (2) сходится в любой точке
ряд (2) расходится. Предположим противное, что ряд (2) сходится в любой точке 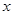 :
:  . Тогда по первой части теоремы ряд (2) должен сходится в точке
. Тогда по первой части теоремы ряд (2) должен сходится в точке 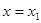 , что против условия
, что против условия 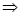 при
при  :
:  , ряд (2) расходится.
, ряд (2) расходится.
|
|
|
Дата добавления: 2014-01-04; Просмотров: 254; Нарушение авторских прав?; Мы поможем в написании вашей работы!