Ряд Фурье для функций любого периода

Теперь рассмотрим вопрос о разложении в тригонометрический ряд функции, период которой отличен от .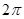

Пусть переодическую функцию 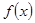с периодом 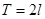, требуется разложить на отрезке длиной 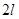(для определенности на 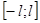). Предполагается, что на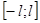 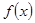удовлетворяет условиям Дирихле.

Обозначим 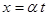и, воспользовавшись свойством 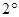переодических функций, подберем такое значение 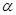, чтобы функция 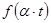независимой переменной 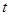имела бы период 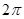. Если 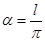, то период 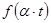будет равен 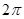т.к. 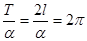. Следовательно, подстановкой 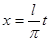, что означает сжатие или растяжение графика функции по 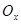, приводит исходную функцию с периодом 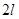к функции 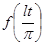с периодом 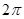, удовлетворяющей условиям Дирихле на 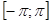. Тогда ряд Фурье и коэффициенты Фурье для этой функции найдутся по формулам:

=

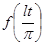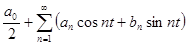
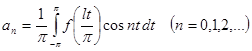
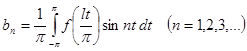
Перейдя к старой переменной 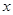и учитывая, что 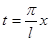и 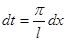, получим ряд Фурье:

=

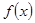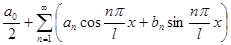
(сходится к 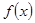с периодом 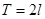на )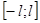

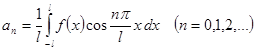
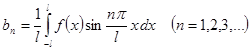
В частном случае, если 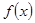- четная с периодом 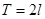, то ряд Фурье для нее получится в виде ряда по :

=

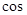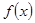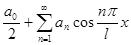
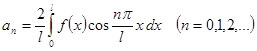
Если 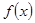- нечетная с периодом 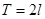, то она раскладывается в ряд Фурье по :

=

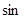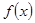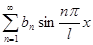
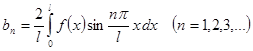
Пример. Разложить в ряд Фурье 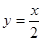на .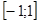

Решение:

Функция 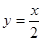нечетна и удовлетворяет условиям Дирихле, 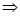её можно разложить в ряд по 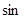. Подсчитаем коэффициенты ряда:

=

.

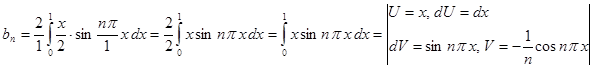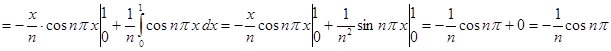Ответ. .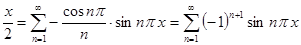

Дата добавления: 2014-01-04