Доказательство. Вопрос 2. Диагностирование механизма газораспределения

Вопрос 2. Диагностирование механизма газораспределения.

Исследования вибраций, формируемых клапанным механизмом системы газораспределения, показали, что с изме­нением теплового зазора существенно изменяется интен­сивность вибрации крышки головки блока в области проверяемого клапана.

Для установки датчиков к двигателю лучше ис­пользовать гайки крепления крышки головки двигателя, они расположены по оси соответствующих цилиндров. Дат­чик устанавливают специальным магнитным устройством или навинчивают. Для оценки и выбора наиболее благо­приятного диагностического режима получены зависимости интенсивности вибрации в дефектационных зонах клапанов каждого цилиндра от теплового зазора при различных ско­ростных режимах работы двигателя.

Уменьшение оборотов до минимально устойчивых зна­чительно снижает рассеивание и повышает стабильность параметров общего уровня вибрации по цилиндрам. При работе двигателя с низкой частотой вращения коленча­того вала создаются лучшие условия для стробирования сигнала.

По интенсивности вибрации импульсов, формируемых ударами при посадке клапанов и выделенных временным селектором, можно определить тепловой зазор в клапанном механизме.

Зафиксируем значение переменной у, считая у = у₀. Тогда функция f (x, y₀) будет функцией одной переменной х, для которой х = х₀ является точкой экстремума. Следовательно, по теореме Ферма 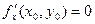или не существует. Аналогично доказывается такое же утверждение для .

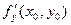Определение. Точки, принадлежащие области определения функции нескольких переменных, в которых частные производные функции равны нулю или не существуют, называются стационарными точками этой функции.

Замечание. Таким образом, экстремум может достигаться только в стационарных точках, но не обязательно он наблюдается в каждой из них.

Примеры.

1. Найдем стационарную точку функции z = x ² + y ². Для этого решим систему уравнений 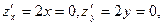откуда х₀ = у₀ = 0. Очевидно, что в этой точке функция имеет минимум, так как при х = у = 0 z = 0, а при остальных значениях аргументов z > 0.
2. Для функции z = xy стационарной точкой тоже является (0, 0), но экстремум в этой точке не достигается (z ( 0, 0) = 0, а в окрестности стационарной точки функция принимает как положительные, так и отрицательные значения).

Теорема 2 (достаточные условия экстремума). Пусть в некоторой окрестности точки М₀ (х₀, у₀), являющейся стационарной точкой функции z = f (x, y), эта функция имеет непрерывные частные производные до 3-го порядка включительно. Обозначим Тогда:

1) f (x, y) имеет в точке М₀ максимум, если AC – B ² > 0, A < 0;

2) f (x, y) имеет в точке М₀ минимум, если AC – B ² > 0, A > 0;

3) экстремум в критической точке отсутствует, если AC – B ² < 0;

4) если AC – B ² = 0, необходимо дополнительное исследование.

Доказательство.

Напишем формулу Тейлора второго порядка для функции f (x, y), помня о том, что в стационарной точке частные производные первого порядка равны нулю:

где Если угол между отрезком М₀М, где М (х₀+ Δ х, у₀+ Δ у), и осью О х обозначить φ, то Δ х = Δ ρ cos φ, Δ y = Δρsinφ. При этом формула Тейлора примет вид: 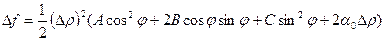. Пусть 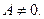Тогда можно разделить и умножить выражение в скобках на А. Получим:

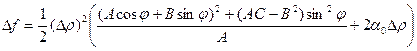. (17.1)

Рассмотрим теперь четыре возможных случая:

1) AC-B ² > 0, A < 0. Тогда 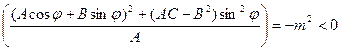, и при достаточно малых Δρ. Следовательно, в некоторой окрестности М₀ f (x₀ + Δ x, y₀ + Δ y) < f (x₀, y₀), то есть М₀ – точка максимума.

2) Пусть AC – B ² > 0, A > 0. Тогда 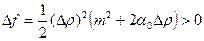, и М₀ – точка минимума.

3) Пусть AC-B ² < 0, A > 0. Рассмотрим приращение аргументов вдоль луча φ = 0. Тогда из (17.1) следует, что , то есть при движении вдоль этого луча функция возрастает. Если же перемещаться вдоль луча 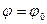такого, что tg φ₀ = -A/B, то 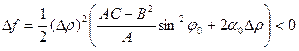, следовательно, при движении вдоль этого луча функция убывает. Значит, точка М₀ не является точкой экстремума.

3`) При AC – B ² < 0, A < 0 доказательство отсутствия экстремума проводится

аналогично предыдущему.

3``) Если AC – B ² < 0, A = 0, то 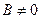. При этом . Тогда при достаточно малых φ выражение 2 B cosφ + C sinφ близко к 2 В, то есть сохраняет постоянный знак, а sinφ меняет знак в окрестности точки М₀. Значит, приращение функции меняет знак в окрестности стационарной точки, которая поэтому не является точкой экстремума.

4) Если AC – B ² = 0, а , , 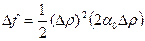то есть знак приращения определяется знаком 2α₀. При этом для выяснения вопроса о существовании экстремума необходимо дальнейшее исследование.

Дата добавления: 2014-01-04