Лекция 26. Составление модели линейного программирования

Классификация экономико-математических моделей

Поскольку менеджеры, преимущественно, имеют дело с экономическими моделями, то рассмотрим их классификацию.

1. По степени агрегирования объектов моделирования модели разделяются на макроэкономические и микроэкономические.

К макроэкономическим относят модели, отражающие функционирование экономики как единого целого.

Микроэкономические модели связаны с такими звеньями экономики как предприятие и фирмы.

1. По предназначению, т.е. по цели создания и применения выделяют:
• имитационные модели, которые предназначены для использования в процессе машинной имитации изучаемых систем или процессов.
• оптимизационные модели, предназначенные для выбора наилучшено варианта из определенного или бесконечного числа вариантов производства, распределения или потребления.
• балансовые модели, выражающие требование соответствия наличия ресурсов и их использования.
• трендовые модели, в которых развитие моделируемой экономической системы отражается через тренд (длительную тенденцию) ее основных показателей
2. По типу информации, используемой в модели, экономико-математические модели делятся на:
• аналитические, построенные по априорной, т.е.известной до опыта информации
• идентифицируемые, построенные на пост априорной информации
3. По учету фактора времени модели подразделяются на:
• статистические, в которых все зависимости отнесены к одному моменту времени
• динамические – которые описывают экономические системы в развитии.
4. По учету фактора неопределенности модели распадаются на:
• детерменированные, если в них результаты однозначно определяются управляющими воздействиями
• стохастические (вероятностные), если на входе, при задании модели определенной совокупности значений, - на ее выходе могут получаться различные результаты в зависимости от действия случайных факторов.

Перечисленные экономико-математические модели могут еще классифицироваться по характеристике математических объектов, включенных в модель т.е. по типу математического аппарата, используемого в модели на:

• матричные модели
• модели линейного и нелинейного программирования
• корреляционно-регрессионные модели
• модели теории массового обслуживания
• модели сетевого планирования
• модели теории игр и т.д.

Например, экономико-математическая модель межотраслевого баланса затрат труда является одновременно макроэкономической, аналитической, балансовой, матричной, детерменированной моделью.

В общем виде задача линейного программирования может быть записана следующим образом:

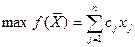(2,3)

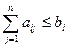
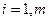(2,4)

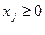j=1,n (2,5)

• где, 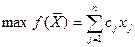называется целевой функцией

• ограничение (2,4) называется функциональными ограничениями.
• Ограничение 2,5) называется прямыми ограничениями или условиями не отрицательности

Рассмотрим получение математической модели и ее решение на примере предприятия

Пусть на предприятии есть две категории рабочих:

• Основные
• Вспомогательные

Нормы затрат труда на производство единицы двуъ видов продукции, наличие трудовых ресурсов на предприятии и цены единиц продукции приведены в таблице

Категория рабочих	Нормы затрат труда на единицу продукции	Наличие ресурсов труда
Продукция 1	Продукция 2
Основные Вспомогательные
Цены единицы продукции

Требуется составить план выпуска продукции при имеющихся ограничениях на трудовые ресурсы. План должен обеспечивать наибольшую общую стоимость выпущенной продукции.

Решение.

Пусть 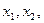- объемы выпуска продукции каждого вида.

Тогда целевая функция задачи имеет вид:

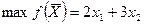
Функциональные ограничения определяются объемами имеющихся трудовых ресурсов:

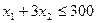
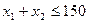
Условия неотрицательности переменных будут

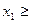0;

;

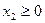Таким образом, получаем задачу линейного программирования (ЗЛП), которую можно решить с помощью электронных таблиц. (на практике)

Лекция по теме:»Процедура поиска решения»

Для решения более трудных задач используется процедура по­иска решения, которая намного сложнее, чем подбор параметра

Инструмент Поиск решения является надстройкой Excel, которая позволяет решать оптимизационные задачи. Ес­ли в меню Сервис отсутствует команда Поиск. решения, значит, нужно загрузить данную надстройку. Для этого выберите команду Сервис^ Надстройки и в раскрывшемся диалоговом окне Над­стройки установить флажок Поиск решения.

Процедура поиска решения позволяет отыскать такое решение задачи (или несколько решений), при котором значение в задан­ной ячейке рабочего листа (в целевой ячейке) достигает максимума или минимума либо равняется определенному числу.

Средство поиска решения, как правило, используется для за­дач, которые удовлетворяют перечисленным ниже условиям:

Значение целевой ячейки зависит от значений других ячеек и формул.

Значения изменяемых ячеек находятся в определенных пре­делах или удовлетворяют определенным ограничениям.

Задача оптимального использования ресурсов

В экономике оптимизационные задачи возникают в связи с

многочисленностью возможных вариантов функционирования конкретного экономического объекта, когда возникает ситуация выбора варианта, наилучшего по некоторому правилу, критерию, характеризуемому соответствующей целевой функцией (например, иметь минимум затрат, максимум продукции).

Например, фабрика имеет в своем распоряжении определенное количество ресурсов:

• рабочую силу,
• деньги,
• сырье,
• оборудование,
• производственные площади и т.п.

Допустим, например, ресурсы трех видов: рабочая сила, сырье и оборудование - имеются в количестве соответственно 80 (чел/дней), 480 (кг) и 130 (станко/ч). Фабрика может выпускать ковры четырех видов. Информация о количестве единиц каждого ресурса, необходимых для производства одного ковра каждого вида, и доходах, получаемых предприятием от единицы каждого вида товаров, приведена в таблице 1.

Таблица 1

Ресурсы Нормы расхода ресурсов на единицу Наличие

продукции_____________________________________ ресурсов

Ковер Ковер Ковер Ковер

___________________ «Лужайка «Силуэт» «Детский» «Дымка»________________

Труд_____________________ 7__________ 2 2 6__________ 80

Сырье___________________ 5__________ 8__________ 4__________ 3__________ 480

Оборудование____________ 2__________ 4___________ 1__________ 8__________ 130

Цена (тыс.руб) | 3 | 4 | 3 | 1 |

Укладываясь в отведенные ресурсы, требуется найти такой план выпуска продукции, при котором будет максимальной общая стоимость выпускаемой продукции.

Обозначим через Х1Х2,Х₃,Х₄ количество ковров каждого типа.

Дата добавления: 2014-01-04