Формула Стокса

Формула Стокса связывает интеграл по поверхности (s) с криволинейным интегралом по контуру (L), ограничивающему эту поверхность:

За положительное направление нормали 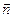к поверхности (s) берется такое направление, чтобы с конца 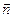обход по контуру L, оставляющий поверхность слева, был виден против часовой стрелки.

В двумерном случае формула Стокса совпадает с формулой Грина.

Циркуляция векторного поля 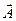по замкнутому контуру 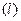равна потоку ротора этого векторного поля через произвольную поверхность 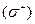, опирающуюся на контур .

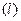Рис. 25.2.

Направление на 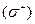и направление на контуре 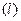образуют “правую систему”.

Используя формулу Стокса в векторной форме, можно дать другое определение ротора поля, эквивалентное первому и не зависящее от выбора координатной системы. Для этого запишем формулу Стокса для достаточно малой плоской площадки S c контуром 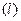, содержащей точку M:

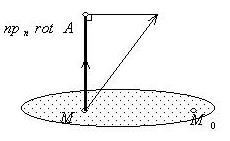
Рис. 25.3.

Поверхностный интеграл в правой части можно записать по теореме о среднем в следующем виде:

,

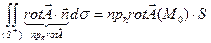где 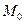- некоторая (средняя) точка площадки S, площадь которой тоже обозначена буквой S.

Тогда из формулы Стокса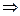

Пусть теперь контур 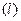стягивается в точку M, тогда 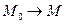и 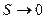. Переходя к пределу при этих условиях, получаем, что 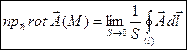Þ Ротор вектора 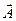в точке M – это вектор, проекция которого на каждое направление равна пределу отношения циркуляции вектора 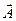по контуру 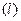плоской площадки S, перпендикулярной этому направлению, к площади этой площадки, стягивающейся в точку.

Очевидно, что из формулы Стокса также следует, что 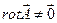означает способность векторного поля совершать работу при перемещении по замкнутому контуру.

Рис. 25.4.

Некоторое физическое истолкование понятия ротора можно получить, если рассматривать векторное поле линейных скоростей 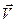твердого тела (материальной точки M), вращающегося вокруг оси 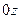с постоянной угловой скоростью .

Из физики известно, что 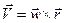, где 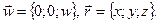Поэтому 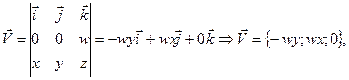т.е. поле линейных скоростей тела, вращающегося вокруг неподвижной оси есть плоское векторное поле и его ротор равен

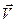т.е. ротор этого поля направлен параллельно оси вращения, его модуль равен удвоенной угловой скорости вращения. Таким образом, характеризует вращательную способность поля 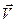, наличие у этого поля “закрученных” векторных линий или “вихрей”.

Дата добавления: 2014-01-04