Исследование устойчивости трубопровода с протекающей жидкостью

Неконсервативные нагрузки на упругие системы, в частности, на трубопроводы возникают со стороны протекающей по ним жидкости. Задача об устойчивости участка трубопровода, по которому протекает жидкость, рассмотрена в известном сборнике задач В.И.Феодосьева. Область устойчивости и частота флаттера здесь определялись путем представления решения уравнения возмущенного движения в виде степенного ряда. В данном параграфе мы построим границу описанными выше методами.

Рассмотрим прямолинейный участок трубопровода, наполненный невязкой жидкостью, которая движется с невозмущенной скоростью 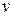. Расчетная схема трубопровода может быть представлена в виде стержня с изгибной жесткостью 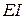, погонной массой 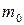и длиной 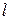. Пусть один конец стержня жестко защемлен в заделке, а другой свободен от закреплений (рис. 1). Плотность протекающей жидкости обозначим через 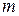, а перемещения сечений стержня при отклонениях от прямолинейной формы равновесия - через .

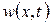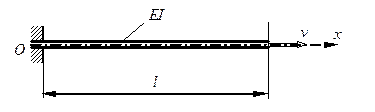
Рис. 1. Расчетная схема участка трубопровода

Будем считать движение жидкости одномерным, а условия на выходе из трубопровода такими, что осевые усилия от потока отсутствуют. При этом можно трактовать жидкость как подвижную нагрузку с интенсивностью сил инерции, равной 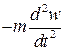. Здесь под оператором 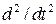понимается полная производная по времени, при вычислении которой необходимо учитывать, что жидкость участвует в двух движениях: движение по трубопроводу со скоростью 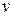и в отклонениях 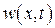от оси 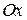вместе с деформациями трубопровода

.

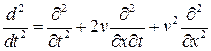Кроме обычной нормальной даламберовой силы, учитываемой первым членом в правой части этого выражения, второй член соответствует кориолисовому ускорению из-за поворота потока частиц жидкости, и третий член связан с центробежными силами, определяемыми кривизной потока при колебаниях трубопровода. Введем в рассмотрение также силы внутреннего трения по модели Фойхта. Оператор внешнего рассеяния энергии считаем пропорциональным инерционному оператору. Тогда уравнение малых колебаний около невозмущенной формы равновесия можно записать в виде

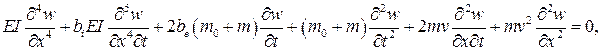
(1)

где 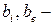параметры внутреннего (фойхтовского) и внешнего трения. Уравнение (1) необходимо дополнить граничными условиями

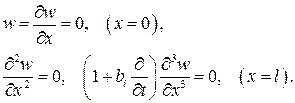(2)

Введем безразмерные параметры

(3)

За параметры нагружения, на плоскости которых будем строить границу области устойчивости прямолинейной формы равновесия трубопровода, будем считать следующие: 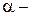параметр, характеризующий расход жидкости и 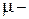относительную погонную массу жидкости. Уравнение (1) относительно 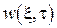и граничные условия (2) с учетом (3) перепишутся следующим образом

(4)

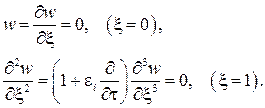(5)

В силу линейности уравнения возмущенного движения (4) представим его решение 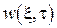в виде

. (6)

Подстановка (6) в уравнение (4) приводит к обобщенной задаче на собственные значения с обыкновенным дифференциальным уравнением

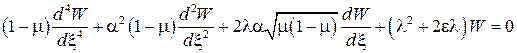(7)

и граничными условиями:

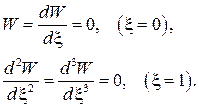(8)

Характеристические показатели 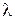, соответствующие нетривиальному решению однородной краевой задаче (7), (8), образуют дискретное множество. Общее решение линейного дифференциального уравнения (7) можно записать в виде

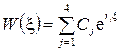, (9)

где 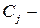некоторые постоянные, 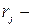показатели, определяемые из алгебраического уравнения

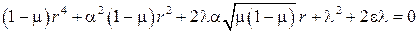. (10)

В общем случае характеристические показатели 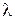являются комплексными, образуя комплексно сопряженные пары. Следовательно, и коэффициенты алгебраического уравнения (10) комплексны, а его корни 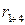уже не являются комплексно сопряженными.

Удовлетворение граничным условиям (8) и требование нетривиальности решения уравнений для 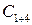приводят к уравнению, определяющую границу области устойчивости в пространстве параметров системы

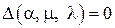, (11)

где

.

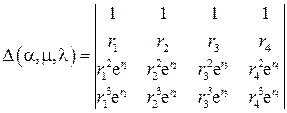Применение метода разложения по формам собственных колебаний приводит к уравнению относительно обобщенных координат 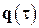вида

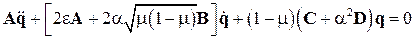, (12)

где матрицы и вычисляются по тем же формулам (см. лекции по УМС), а матрица 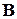по формуле

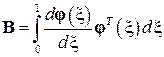
или в индексных выражениях для элементов матрицы 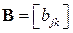, 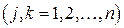можно записать

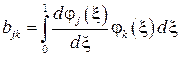
Коэффициенты характеристического полинома для рассматриваемой задачи суть следующие матрицы

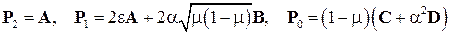. (13)

Как показали вычисления, при определенных сочетаниях параметров потока жидкости в системе возможна потеря устойчивости только колебательного типа, т.е. флаттер. На рис. 2 для коэффициентов демпфирования 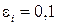и на плоскости относительная масса жидкости 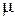– расход жидкости 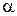приведены результаты вычислений границы области устойчивости двумя вышеизложенными методами. Точная граница флаттера, построенная с использованием уравнения (11), показана сплошной линией. Область устойчивости расположена ниже этой линии. Пунктирные, штриховая и штрихпунктирная линии соответствуют вычислениям при различном числе членов ряда в разложении прогиба в ряд, о чем свидетельствуют числа, стоящие у кривых. Из рисунка следует, что граница флаттера имеет достаточно сложную конфигурацию с наличием участков немонотонной зависимости 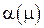. Чтобы достаточно точно построить границу при использовании метода разложения по собственным формам колебаний необходимо удержание не менее восьми членов ряда.

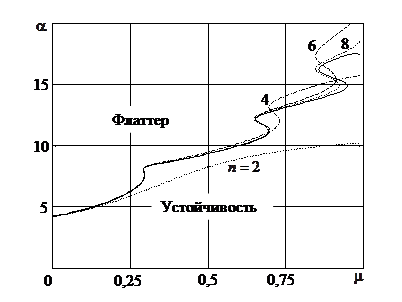
Рис. 2. Граница области устойчивости для участка трубопровода с протекающей жидкостью

Дата добавления: 2014-01-04