Интегралы, зависящие от параметров

Интегралы вида 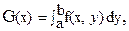х=(х₁, х₂, …, х_m) называются интегралами, зависящими от параметров х₁, х₂, …, х_m.

Теорема 29.3.

Пусть функция f(x,y), х=(х₁, х₂, …, х_m) непрерывна на множестве a£y£b, xÎA, где А – замкнутое ограниченное множество. Тогда интеграл является непрерывной функцией на множестве А.

Если m=1, то в качестве множества А в теореме можно взять сегмент [c,d]. Рассмотрим теперь, при каких условиях интегралы, зависящие от параметров, можно дифференцировать по параметрам. Для простоты ограничимся случаем интегралов G(x), которые зависят от одного параметра.

Теорема 29.4.

Пусть причем функция f(x,y) и частная производная непрерывны при уÎ[a,b], xÎ[c,d]. Тогда на сегменте [c,d] существует производная 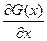и ее можно вычислить, производя дифференцирование под знаком интеграла, т.е. .

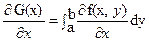Аналогично можно для интегралов, зависящих от нескольких параметров, доказать следующую теорему: пусть 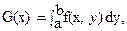х=(х₁, х₂, …, х_m) причем функция f(x,y) и частная производная непрерывны при уÎ[a,b], хÎА, где А – выпуклое замкнутое ограниченное множество. Тогда на множестве А существует частная производная и ее можно вычислить, производя дифференцирование под знаком интеграла, т.е. .

Рассмотрим интегралы вида 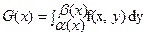. Если функция f(x,y) и частная производная непрерывны при уÎ[a,b], хÎА, а функции a(х) и b(х) имеют частные производные по переменной х_k, то .

При интегрировании по параметру интеграла, зависящего от параметра, используется следующая теорема.

Теорема 29.5.

Пусть функция f(x,y) непрерывна при с£х£d, a£y£b и тогда при вычислении интеграла можно производить интегрирование по параметру под знаком интеграла, определяющего функцию G(x), т.е. .

Пример 29.3.

Функция cos(ux) непрерывна в плоскости IR². Следовательно функция j(u)=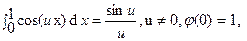непрерывна всюду. Значит, 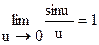, т.е. мы опять получаем первый замечательный предел

Пример 29.4.

Пусть f(x,t)=x^t, xÎ[0,1], tÎ[a,b] (a³0, b>0]; можно согласно теореме 3 составить равенство 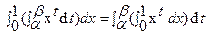. Вычисляя внутренние интегралы, находим значение определенного интеграла .

Это значение трудно найти обычными приемами интегрирования, поскольку неопределенный интеграл от 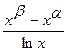не выражается в элементарных функциях.

Пример 29.5.

Интеграл (t>0) не вычисляется обычными приемами. Однако в силу теоремы 2 (ее условие здесь выполнено) имеем (здесь первообразная вычисляется c помощью замены переменной tgx=u). Интегрируя по переменной t, можно восстановить значение интеграла G(t): .

Чтобы найти значение С, в равенстве , справедливом при всех t>1, будем переходить к пределу при t®¥ или при t=1/t®0. Заметим, что функция ln(1+t²sin²x) определена и непрерывна в прямоугольнике 0£х£p/2, 0£t£t₀<1, поэтому, в силу теоремы 1, функция Ф(t)=непрерывна при 0£t£t₀.

Следовательно, 0=Ф(0)=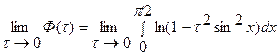с другой стороны, 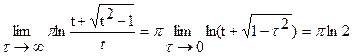. Окончательно с=-pln2 и .

Ортогональность функций

Пусть даны две функции f(x) и g(x), произведение которых интегрируемо на отрезке [a,b].

ОПРЕДЕЛЕНИЕ 29.3. Функции f(x) и g(x), называются ортогональными на [a,b], если

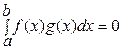
ОПРЕДЕЛЕНИЕ 29.4. Функциональная последовательность

называется ортогональной на , если ,

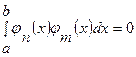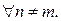
ОПРЕДЕЛЕНИЕ 29.5. Функциональная последовательность 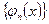называется ортонормированной на , если

Приведём пример ортогональной последовательности.

Пример 29.6.

Докажем, что последовательность тригонометрических функций 1, cos(x), sin(x), cos(2x), sin(2x),…, cos(nx), sin(nx), … (1) ортогональна на отрезке.

С этой целью вычислим интегралы: ,

;

при m ≠ n.

Если же m = n, то 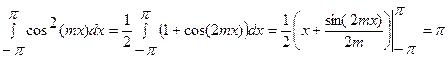. Следовательно,

Аналогичным образом устанавливаем, что

Остаётся вычислить интеграл

Поскольку подынтегральная функция является нечётной, то . Из равенств данного примера следует, что любые две различные функции из последовательности ортогональны на отрезке .

Ряд Фурье и его коэффициенты.

Члены тригонометрического ряда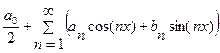

являются периодическими функциями с общим периодом 2, поэтому и сумма этого ряда S (x) также будет 2π – периодическая функция.

Возникает вопрос: любую ли периодическую с периодом 2π функции можно представить в виде тригонометрического ряда (1)? Ответ на этот вопрос дадим позднее.

Теперь же допустим, что 2π – периодическую функцию f (x) можно разложить в тригонометрический ряд (1), равномерно сходящийся на отрезке .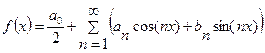

Рассмотрим вопрос об определении коэффициентов , 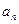и . Для этого применим теорему о почленном интегрировании функционального ряда. Проинтегрируем обе части равенства 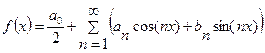в пределах от -π до π: .

Из равенств 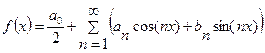следует, что все интегралы, встречающиеся в правой части под знаком суммы равны нулю, поэтому .

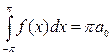Следовательно, _.

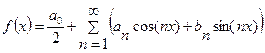Для того чтобы найти обе части равенства умножим на cos(mx) и проинтегрируем на отрезке :

Поскольку система тригонометрических функций, как мы убедились ранее, является ортогональной, то 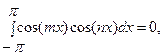для 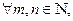если m ≠ n.

Это означает что все с интегралы, встречающиеся в правой части, будут равны нулю; исключение составляет интеграл, который получается при m = n. Этот интеграл равен

Поэтому 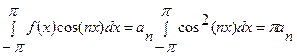, откуда 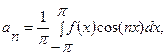n =1,2,…

Аналогично, умножив обе части равенства 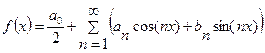на sin(mx) и проинтегрировав на отрезке 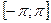, получаем, что , n =1,2,…

Итак, если функцию f(x) можно представить в виде тригонометрического ряда 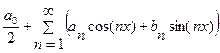, то коэффициенты , , 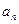вычисляются по формулам

_, , .

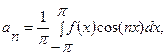ОПРЕДЕЛЕНИЕ 29.6. Числа , , 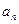называются коэффициентами Фурье для функции f(x), а тригонометрический ряд (2) с такими коэффициентами – рядом Фурье для f(x).

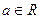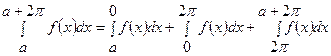Докажем, что промежуток интегрирования для периодической с периодом 2функции можно заменить любым промежутком , , длина которого равна 2. Действительно,. Если в последнем интеграле произвести замену переменной по формуле , dx = dt, то . Так как из-за периодичности функции .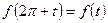

Поэтому .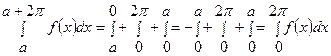

Если вместо а подставим , то получим .

Таким образом, коэффициенты Фурье можно вычислить по формулам

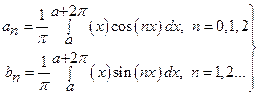
Из чего вытекает, что для любой интегрируемой на 2- периодической функции можно вычислить её Фурье коэффициенты. Следовательно, для такой функции можно составить ряд Фурье .

Такая запись означает, что функция только формально записана в виде ряда Фурье; остаётся неясным, будет ли сумма этого ряда равна функции . Вопрос: каким условиям должна удовлетворять функция , чтобы её ряд Фурье сходился к ?

ОПРЕДЕЛЕНИЕ 29.7. Функция f(x) называется кусочно-гладкой на отрезке [a,b] если функция f(x) и её производная на [a,b] имеют конечное число точек разрыва первого рода.

Без доказательства приведём теорему, которая даёт достаточные условия разложимости функции в ряд Фурье.

Теорема 29.6. (Дирихле). Если f(x) – периодическая с периодом 2кусочно-гладкая на функция, то её ряд Фурье сходится в любой точке этого отрезка и его сумма равна:

1) функция f(x), когда x – точка непрерывности функции f(x);

2) 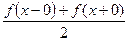, когда x – точка разрыва функции f(x)

.

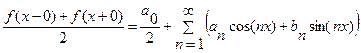Отметим, что на практике чаще всего имеем дело с функциями, которые удовлетворяют условиям теоремы Дирихле.

Пример29.7.

Периодическую с периодом функцию разложить в ряд Фурье.

Вычислим коэффициенты Фурье:

; ,

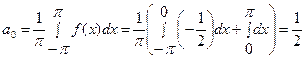Данная функция f(x) удовлетворяет условиям теоремы Дирихле, её график изображён на рис.29.1.

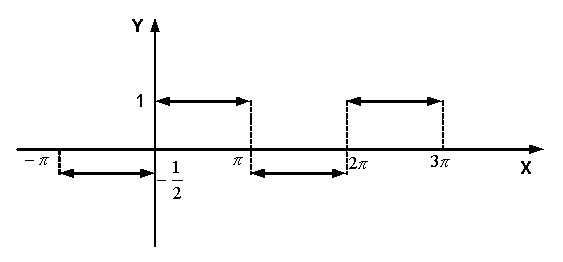
Рис.29.1.

Следовательно, .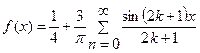

Дата добавления: 2014-01-04