Понятие интеграла Фурье

Предположим, что функция f(x) является кусочно-гладкой и периодической с периодом 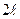, кроме того, определим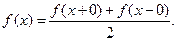

Тогда периодическая функция f(х) является непрерывной и имеет непрерывную производную на всей числовой оси, за исключением, может быть, конечного числа точек на отрезке . Кроме того, в этих точках существуют конечные пределы 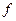и 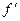слева и справа. Множество обладающих такими свойствами функций обозначим через L¹.

Каждую 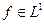можно представить рядом Фурье

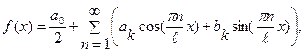
коэффициенты которого определяются по формулам:

,

, .

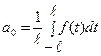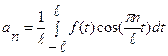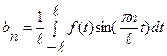Исследуя ряд Фурье, мы доказали, что ряд Фурье функции 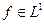сходится к f(x).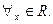

Предположим, что функция f является непериодической кусочно-гладкой на любом конечном отрезке вещественной числовой оси и абсолютно интегрируема на ней.

Множество кусочно-гладких на вещественной оси функций обозначим через L¹ 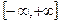. Кроме того, как и в случае периодических функций, определим .

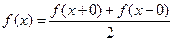Выражение интеграла Фурье получим из ряда Фурье периодической функции .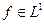

Для этого в ряд 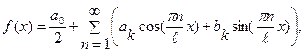подставим выражения коэффициентов 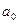, 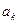и .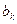

Имеем: .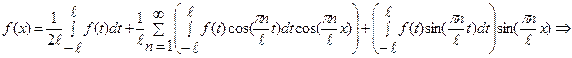

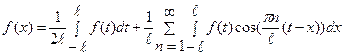Вводим обозначения: .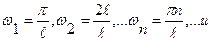

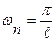Тогда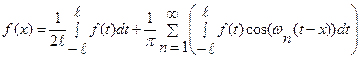

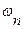
Пусть 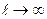(функция f из периодической становится не периодической).

Очевидно, что ,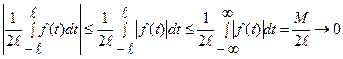

Второе слагаемое из выражения 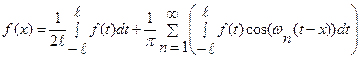с

учётом обозначения 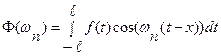приводим к виду

∆∆.

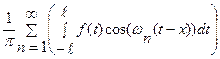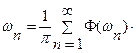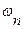В таком виде эта сумма напоминает интегральную сумму функции Ф (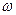) на отрезке .

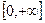Перейдя к пределу 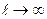, получаем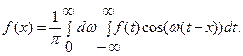

Это выражение назовём двойным интегралом Фурье для непериодической функции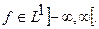

Замечание. Интегральная сумма 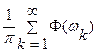∆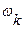отличается от классической интегральной суммы тем, что в этой интегральной сумме значения 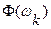меняются с изменением 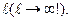Поэтому предельный переход 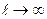требует соответствующего обоснования. Однако этого теоретического вопроса касаться не будем.

Пример 30.4.

Представить функцию

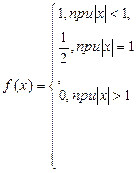
интегралом Фурье.

Очевидно, что эта функция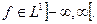

Поэтому

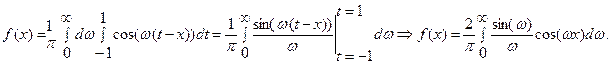
Так как f(0)=1, то .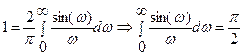

Итак, используя интеграл Фурье, получили интересный результат. Напомним, что первообразная функция 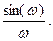не может быть выражена в конечном виде.

Выражение 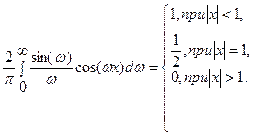называется разрывным множителем Дирихле.

Преобразуем интеграл Фурье следующим образом:

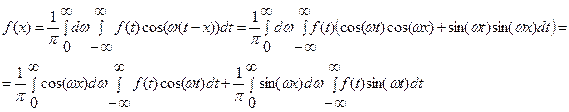
Обозначим: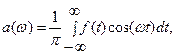

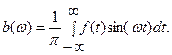
Тогда .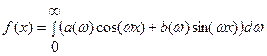

В таком виде интеграл Фурье похож на ряд Фурье. Суммирование по дискретному параметру 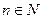заменено интегрированием по непрерывно меняющемуся параметру 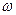. Коэффициенты 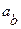и 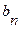аналогичны коэффициентам 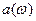и .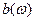

Дата добавления: 2014-01-04