Якобиан и его геометрический смысл

Рассмотрим общий случай замены переменных в двойном интеграле. Пусть в плоскости О ху дана область D, ограниченная линией L. Предположим, что х и у являются однозначными и непрерывно дифференцируемыми функциями новых переменных u и v:

x = φ(u, v), y = ψ(u, v). (25.8)

Рассмотрим прямоугольную систему координат О uv, точка Р΄(u, v) которой соответствует точке Р(х, у) из области D. Все такие точки образуют в плоскости О uv область D΄, ограниченную линией L΄. Можно сказать, что формулы (9.6) устанавливают взаимно однозначное соответствие между точками областей D и D΄. При этом линиям u = const и

v = const в плоскости О uv будут соответствовать некоторые линии в плоскости О ху.

v y u u+Δu

•P

v+Δv v+Δv

v •P′

v

O u u+Δu u O x

Рис. 4.

Рассмотрим в плоскости О uv прямоугольную площадку Δ S΄, ограниченную прямыми u = const, u+Δu = const, v = const и v+Δv = const. Ей будет соответствовать криволинейная площадка Δ S в плоскости О ху (рис.4). Площади рассматриваемых площадок тоже будем обозначать Δ S΄ и Δ S. При этом Δ S΄ = Δu Δv. Найдем площадь Δ S. Обозначим вершины этого криволинейного четырехугольника Р₁, Р₂, Р₃, Р₄, где

P₁(x₁, y₁), x₁ = φ(u, v), y₁ = ψ(u, v);

P₂(x₂, y₂), x₂ = φ(u+Δu, v), y₂ = ψ(u+Δu, v);

P₃(x₃, y₃), x₃ = φ(u+Δu, v+Δv), y₃ = ψ(u+Δu, v+Δv);

P₄(x₄, y₄), x₄ = φ(u, v+Δv), y₄ = ψ(u, v+Δv).

Заменим малые приращения Δ u и Δ v соответствующими дифференциалами. Тогда

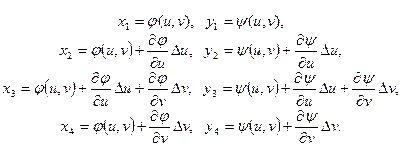
При этом четырехугольник Р₁ Р₂ Р₃ Р₄ можно считать параллелограммом и определить его площадь по формуле из аналитической геометрии:

(25.9)

Определение. Определитель 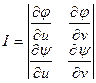называется функциональным определителем или якобианом функций φ(х, у) и ψ(х, у).

Переходя к пределу при в равенстве (25.9), получим геометрический смысл якобиана:

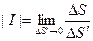, (25.10)

то есть модуль якобиана есть предел отношения площадей бесконечно малых площадок Δ S и Δ S ΄.

Замечание. Аналогичным образом можно определить понятие якобиана и его геометрический смысл для п -мерного пространства: если x₁ = φ₁(u₁, u₂,…,u_n), x₂ = φ₂(u₁, u₂,…,u_n),…, x_n = φ(u₁, u₂,…, u_n), то

(25.11)

При этом модуль якобиана дает предел отношения «объемов» малых областей пространств х₁, х₂,…, х_п и u₁, u₂,…, u_n.

Дата добавления: 2014-01-04