
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Геометрическая интерпретация производной для случая функции двух переменных
|
|
|
|
Касательная – это предельное положение секущей 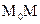 при стремлении при стремлении  к нулю. к нулю.  – касательная к кривой K в точке – касательная к кривой K в точке 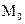 (рис. 38.1), если расстояние (рис. 38.1), если расстояние  от переменной точки M до прямой от переменной точки M до прямой  при при 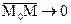 является бесконечно малой высшего порядка, чем является бесконечно малой высшего порядка, чем  (то есть (то есть 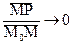 , а это значит, что стремится к нулю , а это значит, что стремится к нулю 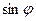 , а с ним и угол , а с ним и угол 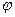 между секущей между секущей 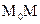 и прямой и прямой  ). ).
| 
|
| Рис. 38.1. |
Рассмотрим теперь некоторую поверхность S и точку 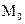 на ней. Дадим определение касательной плоскости.
на ней. Дадим определение касательной плоскости.
Определение 38.1. Плоскость  называется касательной плоскостью к поверхности S в точке
называется касательной плоскостью к поверхности S в точке 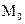 на ней, если расстояние
на ней, если расстояние  от переменной точки
от переменной точки 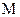 поверхности S до этой плоскости при стремлении
поверхности S до этой плоскости при стремлении 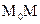 к нулю является бесконечно малой высшего порядка, чем
к нулю является бесконечно малой высшего порядка, чем  (то есть
(то есть 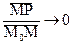 ).
).
Рассмотрим условия, задающие касательную плоскость и нормаль к поверхности. Пусть поверхность S задана уравнением  , точка
, точка  принадлежит этой поверхности. При каких условиях плоскость P, проходящая через точку
принадлежит этой поверхности. При каких условиях плоскость P, проходящая через точку 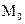 и имеющая уравнение
и имеющая уравнение
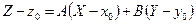 , (38.4)
, (38.4)
удовлетворяет определению 38.1?
Проведём 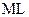 || Oz,
|| Oz,  (рис. 38.2). Рассмотрим отношение
(рис. 38.2). Рассмотрим отношение 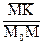 . Если при
. Если при 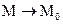
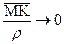 , то и
, то и 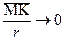 (так как
(так как  ). Отрезок
). Отрезок 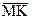 с точностью до знака, равен выражению
с точностью до знака, равен выражению 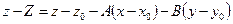 . Если ввести обозначения
. Если ввести обозначения 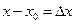 ,
, 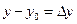 ,
, 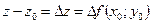 , то выражение перепишется в виде
, то выражение перепишется в виде  .
.
 ,
,
 ,
,
отсюда 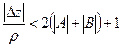 , следовательно
, следовательно
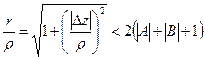 .
.
Таким образом, плоскость (38.4) будет касательной плоскостью к поверхности в том и только в том случае, если 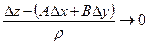 вместе с вместе с  , то есть если , то есть если  .
Для того, чтобы поверхность .
Для того, чтобы поверхность  в точке в точке  , где , где 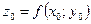 имела касательную плоскость, необходимо и достаточно, чтобы при имела касательную плоскость, необходимо и достаточно, чтобы при  , ,  функция функция  была дифференцируема. Так как при выполнении этого условия A и B равны частным производным была дифференцируема. Так как при выполнении этого условия A и B равны частным производным  и и 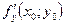 , то касательная плоскость выразится уравнением , то касательная плоскость выразится уравнением
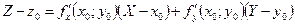 . .
| 
|
| Рис. 38.2. |
Если поверхность задана уравнением 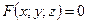 , то касательная плоскость к поверхности в точке
, то касательная плоскость к поверхности в точке  определяется так:
определяется так:
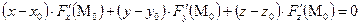 . (38.4а)
. (38.4а)
Нормаль к поверхности в точке  (прямая, проходящая через точку
(прямая, проходящая через точку 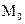 перпендикулярно к касательной плоскости):
перпендикулярно к касательной плоскости):
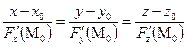 . (38.5)
. (38.5)
Точки, в которых все частные производные функции обращаются в нуль, называются особыми точками функции. В таких точках поверхность не имеет ни касательной плоскости, ни нормали.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 500; Нарушение авторских прав?; Мы поможем в написании вашей работы!