Обозначим через наибольший предел последовательности чисел (40.4.) . Тогда радиус сходимости степенного ряда (40.1.) определяется по формуле

Определение радиуса сходимости

Отправляясь от коэффи­циентов степенного ряда (40.1.), образуем последовательность чисел:

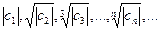(40.4.)

Все члены этой последовательности* рассматриваются как действи­тельные неотрицательные числа.

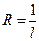(40.5.)

Формула (40.5.) носит название формулы Коши-Адамара.

Замечание.

В случае 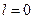в формуле (40.5.) нужно положить , в случае 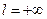необходимо принять .

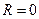При выводе формулы (40.5.) мы рассмотрим отдельно три случая:

1) ,

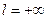
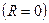2),

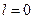
3) .

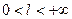
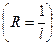Случай 1.

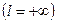последовательность чисел (40.4.) неограничен­ная. Нам нужно доказать, что степенной ряд (40.1.) расходится во вся­кой точке , отличной от нулевой точки. Допуская противное, пред­положим, что ряд (40.1.) сходится в некоторой точке 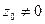. Тогда имеем: 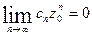; следовательно, существует постоянное положительное число 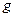такое, что выполняется неравен­ство 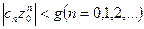. Мы можем предполагать число 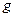большим единицы. Из последнего неравенства путём извлечения из обеих его частей корня 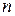-й степени следует: , или 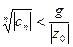, так как 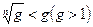. Таким образом, последо­вательность чисел (40.4.) оказывается ограниченной. Полученное про­тиворечие убеждает нас в расходимости ряда (40.1.) при любом .

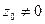Случай 2.

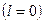нам нужно показать, что ряд (40.1.) сходится в любой точке 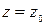. Так как последовательность чисел (40.4.) схо­дится к нулю, то, начиная с достаточно большого 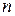, имеем:

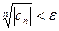, например 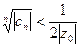, откуда 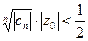, или, по возведении в степень :

.

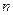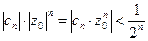Так как ряд с общим членом 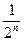сходится, то абсолютно сходится и рядс общим членом .

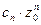Если, наконец, 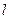есть конечное число, отличное от нуля, то дока­зательство формулы (40.5.) сводится к следующему: ряд (40.1.) абсолютно сходится при любом 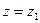, для которого 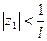, и расходится для каждого 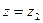, для которого .

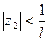Так как 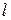есть наибольший предел последовательности чисел (40.4.), то имеем, начиная с достаточно большого :

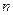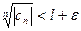(40.6.)

где 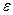— сколь угодно малое положительное число.

Заметив, что 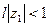, положим 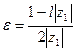. Неравенство (40.6.) примет вид ,

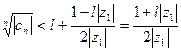или

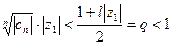(40.7.)

Возводя обе части неравенства (40.7.) в степень ,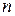

найдём:

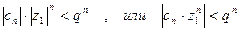. (40.8.)

Так как ряд с общим членом 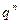, , 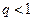сходится, то в силу (40.8.) абсолютно сходится данный степенной ряд при .

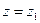С другой стороны, из определения 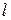как предельного числа последовательности чисел (40.4.) следует, что при бесконечно многих значениях 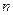имеем:

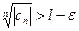(40.9.)

где 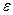– сколь угодно малое положительное число.

Заметив, что 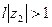, положим 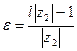. Неравенство (40.9.) перепишется так:

,

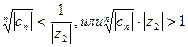что по возведении в степень 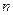даёт: .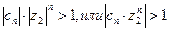

Так как последнее неравенство имеет место для бесконечного мно­жества значений 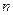, то 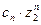не может стремиться к нулю при не­ограниченном возрастании .

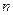Отсюда следует расходимость данного ряда (40.1.) при .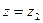

Примеры 40.1.

Радиус сходимости ряда 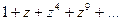равен еди­нице. В самом деле, здесь 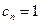, если 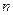–квадрат целого числа, и равно 0 в противном случае. Таким образом, 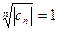или 0, смотря по тому, имеем ли мы первый или второй случай. Предельные числа последовательности(40.4.)будут 0 и 1. Следовательно, 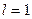и .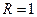

Примеры 40.2.

Радиус сходимости ряда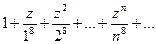

равен единице. Действительно, .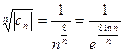

Так как 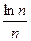стремится к нулю при 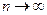, то 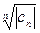стремится к единице.

Следовательно, 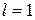и .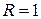

Примеры 40.3.

Ряд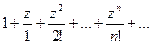

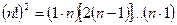сходится во всей плоскости комплексного переменного. Действительно, . Каждая скобка правой части последнего равенства не меньше 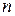, так как имеем:

.

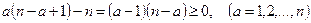Следовательно, получаем , т. е.

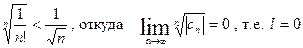
Следовательно, ,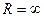

Примеры 40.4.

Ряды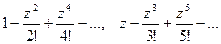

сходятся во всей плоскости комплексного переменного , а ряд 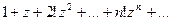сходится лишь в нулевой точке .

Мы указывали, что на окружности круга сходимости степенной ряд в разных случаях может вести себя различно.

Так, взяв пример 40.2. при 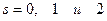, получаем три ряда, для которых :

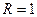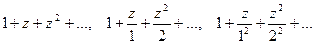
Первый ряд расходится во всех точках окружности 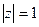; послед­ний сходится во всех точках этой окружности, а второй ряд схо­дится в одних точках этой окружности (например, при 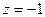) и расходится в других (при ).

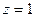Исследованию вопроса о сходимости степенного ряда на окруж­ности его круга сходимости посвящены многочисленные работы, в которых даётся освещение этой проблемы с различных точек зрения.

Дата добавления: 2014-01-04