Признаки сравнения

Операции с каталогами

Имя пути

Иерархические каталоговые системы

Двухуровневые каталоговые системы

Одноуровневые каталоговые системы

Каталоги

В этой системе все файлы содержатся в одном каталоге.

Преимущества системы:

· Простота

· Возможность быстро найти файл, не надо лазить по каталогам

Недостатки системы:

· Различные пользователи могут создать файлы с одинаковыми именами.

Для каждого пользователя создается свой собственный каталог.

Пользователь, при входе в систему, попадает в свой каталог и работает только с ним. Это делает проблематичным использование системных файлов.

Эту проблему можно решить созданием системного каталога, с общим доступом.

Если у одного пользователя много файлов, то у него тоже может возникнуть необходимость в файлах с одинаковыми именами.

Каждый пользователь может создавать столько каталогов, сколько ему нужно.

Почти все современные универсальные ОС, организованы таким образом. Специализированным ОС это может быть не нужным.

Для организации дерева каталогов нужен некоторый способ указания файла.

Два основных метода указания файла.

Абсолютное имя пути – указывает путь от корневого каталога, например:

· для Windows c:\usr\ast\mailbox

· для *NIX /usr/ast/mailbox

· - для MULTICS >usr>ast>mailbox

Относительное имя пути - путь указывается от текущего каталога. Тогда обычно./ – означает текущий каталог;../ – означает родительский каталог

Основные системные вызовы для работы с каталогами:

· Create - создать каталог

· Delete - удалить каталог

· OpenDir - закрыть каталог

· CloseDir - закрыть каталог

· ReadDir - прочитать следующий элемент открытого каталога

· Rename - переименование каталога

· Link - создание жесткой ссылки, позволяет файлу присутствовать сразу в нескольких каталогах.

· Unlink - удаление ссылки из каталога

Теорема 39.1 (1-й признак сравнения). Если для двух рядов с положительными членами

u ₁ + u ₂ +…+ u_n +… (39.1)

и v ₁ + v ₂ +…+ v_n +… (39.2)

выполнено условие u_n ≤ v_n, то:

а) если ряд (39.2) сходится, то сходится и ряд (39.1);

б) если ряд (39.1) расходится, то расходится и ряд (39.2).

Доказательство. Пусть частичная сумма ряда (39.1) , частичная сумма ряда (39.2) . Из условия теоремы следует, что s_n ≤ σ_n. Пусть Ряд (39.2) сходится. Тогда существует конечный предел его частичных сумм: Но s_n ≤ σ_n < σ, то есть последовательность частичных сумм ряда (39.1) ограничена сверху. Следовательно, по теореме (38.6) ряд (39.1) сходится.

Теперь предположим, что ряд (39.1) расходится. Тогда 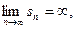σ_n ≥ s_n, значит,

, то есть ряд (39.2) тоже расходится. Теорема доказана.

Следствие. Условие u_n ≤ v_n может выполняться начиная не обязательно с п = 1. Утверждение теоремы справедливо, если это условие выполняется для всех п, больших некоторого N (см. теорему 38.1).

Пример. Исследуем на сходимость ряд , сравнив его с рядом . Этот ряд сходится, так как последовательность его членов представляет собой бесконечно убывающую геометрическую прогрессию со знаменателем , сумма которой равна . При любом n > 1 n ∙ 2 ⁿ > 2 ⁿ, следовательно, 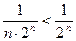, поэтому по теореме 38.2 исследуемый ряд сходится.

Теорема 39.2 (2-й признак сравнения). Если для рядов (39.1) и (39.2) выполнено условие

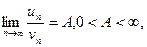то ряды (39.1) и (39.2) сходятся и расходятся одновременно.

Доказательство. Выберем число N такое, что для всех n > N выполняется неравенство

Тогда u_n < (A + 1) v_n. Если ряд сходится, то по теореме 38.2 сходится и ряд , следовательно, по теореме 39.1 сходится ряд . Наоборот, из расходимости ряда следует при этом расходимость .

Теперь выберем число А такое, что 0 < A < A, и зададим номер N, при котором 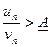при любом n > N. Отсюда u_n > A v_n, и, проводя рассуждения, аналогичные предыдущим, можно показать, что из сходимости следует сходимость , а из расходимости - расходимость . Теорема доказана полностью.

Следствие. При применении 2-го признака сравнения удобно брать в качестве ряда, с которым сравнивается данный ряд, ряд вида (см. пример в начале лекции). Напомним еще раз, что такой ряд сходится при α > 1 и расходится при α ≤ 1.

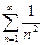Пример. Общий член ряда можно представить в виде (разделив числитель и знаменатель на х). Теперь очевидно, что . Поскольку ряд сходится (так как α = 2 >1), сходится (по теореме 39.2) и исходный ряд.

Дата добавления: 2014-01-04