Признак Лейбница

Если знакопеременный ряд не обладает абсолютной сходимостью, то требуется ответить на вопрос, будет ли он сходиться хотя бы условно. Ответ на него можно дать, применяя признак Лейбница:

Теорема 39.6. Если исследуемый ряд:

1) знакочередующийся, то есть имеет вид u ₁ – u ₂ + u ₃ – u ₄ +…, где u_i > 0; (39.4)

2) u ₁ > u ₂ > u ₃ >… > u_n > u_{n+ 1} >… (последующий член ряда по модулю меньше предыдущего);

3)

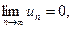
то ряд сходится (хотя бы условно), его сумма положительна и .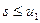

Доказательство. Рассмотрим первых 2 т членов ряда:

s _{2 m} = (u ₁ – u ₂) + (u ₃ – u ₄) +…+ (u _{2 m -1} – u _{2 m} ) > 0,

так как u _{2 i- 1} – u _{2 i} > 0. Итак, последовательность { s _{2 m} } положительна и возрастает с возрастанием т. С другой стороны, s _{2 m} можно записать в ином виде:

s _{2 m} = u ₁ – (u ₂ – u ₃) – (u ₄ – u ₅) -…- (u _{2 m- 2} – u _{2 m- 1}) – u _{2 m} < u ₁.

Следовательно, последовательность { s _{2 m} } ограничена сверху и поэтому имеет предел:

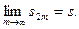
Докажем, что тот же предел имеет и последовательность частичных сумм, составленных их нечетного числа слагаемых:

Таким образом, при любом п, то есть ряд (39.4) сходится.

Пример. Исследуем на абсолютную и условную сходимость ряд .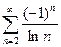

| u_n | = (так как ln n < n), поэтому по первому признаку сравнения ряд 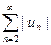расходится, то есть абсолютной сходимостью рассматриваемый ряд не обладает.

Проверим для него выполнение условий теоремы 39.6. Знакочередование обеспечивается множителем (-1) ^п, 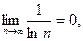а из монотонного возрастания функции

y = ln x следует, что ln(n + 1) > ln n, a . Следовательно, по признаку Лейбница ряд 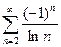сходится условно.

Дата добавления: 2014-01-04