Вторая теорема Абеля

Сумма степенного ряда есть функция, непрерывная при, каково бы ни было,, а значит, и при, т.е. внутри всего круга сходимости.

Итак, степенной ряд, для которого , изображает непрерывную функцию внутри его круга сходимости.

Мы видели,что степенной ряд

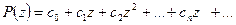(42.1а.)

может сходиться в точках, лежащих на окружности его круга схо­димости. Во всякой такой точке 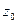, , 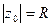функция 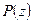имеет определённое конечное значение, и возникает вопрос: каким образом это значение 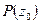связано со значениями 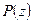в точках 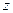, внутрен­них к кругу сходимости?

На этот вопрос даёт ответ следующая теорема, принадлежащая Абелю:

Если степенной ряд (42.1а.) сходится в точке 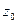окружности его круга сходимости, то его сумма 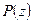стремится к пределу 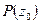, когда точка 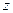стремится к 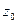, оставаясь на радиусе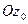

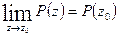
Другими словами, сумма 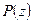ряда (42.1а.) есть функция, непре­рывная в точке 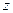вдоль радиуса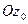

Не уменьшая общности теоремы, мы можем предполагать радиус сходимости равным единице и 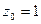. Действительно, полагая 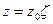, получим 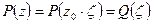, причём радиус сходимости преобра­зованного ряда 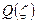будет единица, потому что неравенство 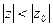равносильно неравенству 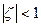; точке 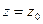будет соответство­вать точка 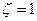. Так как по условию ряд (42.1а.) сходится при 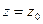, то ряд 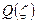будет сходящимся при 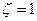. Далее, мы можем ради простоты предполагать 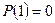, так как в противном случае вместо 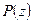взяли бы 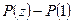. Итак, пусть данный ряд (4.1а.) имеет радиус сходимости 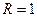и сходится в точке 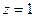к значе­нию 0.

Нужно доказать, что

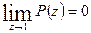(42.2.)

если 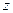остаётся положительным' и 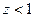. Рассмотрим вспомогатель­ный ряд

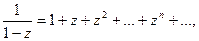(42.3.)

радиус сходимости которого тоже равен единице. Перемножая ряды (42.1а.) и (42.3.), что возможно в силу их абсолютной сходимости при ,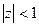

получим:

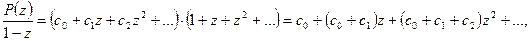
или

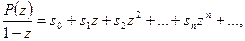(42.4.)

где 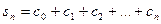представляет частичную сумму ряда .

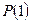Ряд (42.4.) имеет радиус сходимости, равный единице. В самом деле, его радиус сходимости 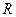не может быть, очевидно, меньше единицы, так как этот ряд получился в результате умножения рядов (42.1а.) и (42.3.) с радиусами сходимости, равными единице; с другой стороны, 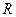не может быть больше единицы, так как в противном случае ряд

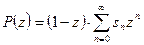(42.5.)

имел бы радиус сходимости больше единицы, что невозможно.

Желая оценить 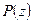, обозначим через 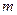натуральное число, пока произвольное, и перепишем (42.5.) в виде

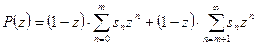(42.6.)

Пусть 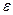— данное сколь угодно малое положительное число. Выбе­рем 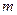столь большим, чтобы при 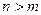имело место неравенство 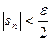, что возможно, так как .

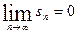Из равенства (42.6.) находим, вспомнив, что 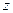– положительное число, меньшее единицы: 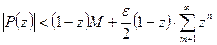где 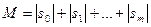и, следовательно, не зависит от .

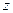Так как 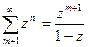, то последнее неравенство имеет вид

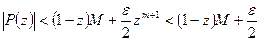(42.7.)

До сих пор 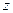было произвольным положительным числом, меньшим единицы. Считая теперь 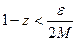из (42.7.) будем иметь: 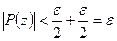что убеждает нас в справедливости теоремы.

Анализируя это доказательство, читатель обнаружит, что теорема справедлива и в том случае, когда 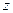любым образом приближается к 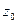, оставаясь внутри какого-либо угла раствора, меньшего 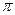, с вер­шиной в точке 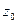и с биссектрисой вдоль радиуса .

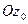Теорема Абеля имеет в анализе многочисленные приложения.

Так, известно, что .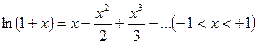

При 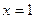этот ряд будет 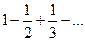и, следовательно, сходится. По доказанной теореме Абеля сумма последнего ряда равна:

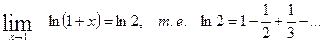
С помощью теоремы Абеля можно распространить теоремуобумножении абсолютно сходящихся рядов на случай рядов, условно сходящихся. Действительно, имея два сходящихся ряда с комплекс­ными членами:

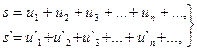(42.8.)

составим их произведение:

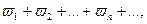(42.9.)

где положено: .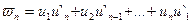

Предположим, что ряд (42.9.) сходится, и обозначим его сумму через . В этом случае можно доказать, что 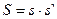, т. е, два любых сходящихся ряда (42.8.) можно перемножить по известному правилу, если в результате получается сходящийся ряд (42.9.).

Для доказательства образуем два степенных ряда:

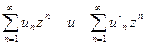(42.9а.)

Так как при 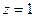по условию оба эти ряда сходятся, то они абсо­лютно сходятся при 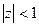. Вследствие этого мы можем их перемножить по известному правилу:

(42.10.)

Так как ряды (42.8.) и (42.9.) сходятся согласно условию, то по второй теореме Абеля имеем:

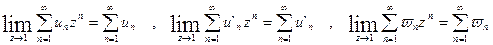
Заметив это, из равенства (42.10.) путём перехода к пределу получим:

.

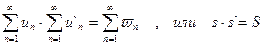Дата добавления: 2014-01-04