
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 43. Линейные однородные дифференциальные уравнения. Определения и общие свойства. Линейные однородные уравнения второго порядка с постоянными коэффициентами
|
|
|
|
Определение 1. Дифференциальное уравнение n – го порядка называется линейным, если оно является уравнением первой степени относительно совокупности искомой функции у и её производных 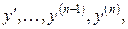 т.е. имеет вид
т.е. имеет вид
 , (1)
, (1)
где  и f(x) – заданные функции от х или постоянные, причем
и f(x) – заданные функции от х или постоянные, причем  для всех значений х из той области, в которой мы рассматриваем уравнение (1).
для всех значений х из той области, в которой мы рассматриваем уравнение (1).
В дальнейшем мы будем предполагать, что функции  и f(x) непрерывны при всех значениях х, причем коэффициент а0 =1. (если он не равен 1, мы можем все члены уравнения поделить на него). Функция f(x), стоящая в правой части уравнения, называется правой частью уравнения.
и f(x) непрерывны при всех значениях х, причем коэффициент а0 =1. (если он не равен 1, мы можем все члены уравнения поделить на него). Функция f(x), стоящая в правой части уравнения, называется правой частью уравнения.
Если  , то уравнение называется линейным неоднородным или уравнением с правой частью. Если же
, то уравнение называется линейным неоднородным или уравнением с правой частью. Если же  , то уравнение имеет вид
, то уравнение имеет вид
 (2)
(2)
и называется линейным однородным. Левая часть этого уравнения является однородной функцией первой степени относительно 
Основные свойства линейных однородных уравнений.
Теорема 1. Если y1 и y2 – два частных решения линейного однородного уравнения второго порядка
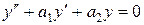 (3)
(3)
то y1 + y2 есть также решение этого уравнения.
Доказательство. Так как y1 и y2 - решения уравнения, то
 и
и  . (4)
. (4)
Подставляя в уравнение (3) сумму y1 + y2 и принимая во внимание тождества (4), будем иметь
 где y1 + y2 есть решение уравнения.
где y1 + y2 есть решение уравнения.
Теорема 2. если y1 есть решение уравнения (3) и С – постоянная, то Су1 есть также решение уравнения (3)
Доказательство. Так как y1 - решения уравнения, то  . Подставляя в уравнение (3) выражение Су1, получим
. Подставляя в уравнение (3) выражение Су1, получим
 ,
,
что и требовалось доказать.
Определение 2. Два решения уравнения (3) y1 и y2 называются линейно независимыми на отрезке 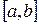 , если их отношение на этом отрезке не является постоянным, т.е. если
, если их отношение на этом отрезке не является постоянным, т.е. если 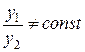 . В противном случае решения называются линейно зависимыми.
. В противном случае решения называются линейно зависимыми.
Иными словами, два решения y1 и y2 называются называются линейно независимыми на отрезке 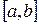 , если существует такое постоянное число
, если существует такое постоянное число 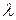 , что
, что 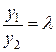 при
при  . В этом случае
. В этом случае 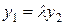 .
.
Пример 1. Рассмотрим уравнение  . Легко проверить, что функция
. Легко проверить, что функция  являются решениями этого уравнения. При этом функции
являются решениями этого уравнения. При этом функции 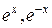 линейно независимы на любом отрезке, т.к.
линейно независимы на любом отрезке, т.к.  не является постоянным при изменении х. Функции
не является постоянным при изменении х. Функции  линей но зависимы, т.к.
линей но зависимы, т.к. 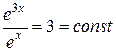 .
.
Определение 3. Если y1 и y2 суть функции от х, то определитель

называется определителем Вронского или вронскианом данных функций.
Определитель Вронского имеет много различных свойств. Нам для доказательства теоремы об общем решении уравнения (3) потребуется следующее свойство:
Теорема 3. Если определитель Вронского  , составленный для решений y1 и y2 линейного однородного уравнения (3), не равен нулю при каком-нибудь значении x=x0 на отрезке
, составленный для решений y1 и y2 линейного однородного уравнения (3), не равен нулю при каком-нибудь значении x=x0 на отрезке 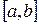 , где коэффициенты уравнения непрерывны, то он не обращается в нуль ни при каком значении х на этом отрезке.
, где коэффициенты уравнения непрерывны, то он не обращается в нуль ни при каком значении х на этом отрезке.
С его помощью мы докажем теорему:
Теорема 4. Если y1 и y2 – два линейно независимых решения уравнения (3), то
 (5)
(5)
где С1 и С2 – произвольные постоянные, есть его общее решение.
Доказательство. Из теорем (1) и (2) следует, что функция 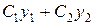 есть решение уравнения (3) при любых значениях С1 и С2.
есть решение уравнения (3) при любых значениях С1 и С2.
Докажем теперь, что каковы бы ни были начальные условия  ,
, , можно так подобрать значения произвольных постоянных С1 и С2, чтобы соответствующее частное решение
, можно так подобрать значения произвольных постоянных С1 и С2, чтобы соответствующее частное решение 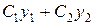 удовлетворяло заданным начальным условиям. Подставляя начальные условия в равенство (5), будем иметь
удовлетворяло заданным начальным условиям. Подставляя начальные условия в равенство (5), будем иметь
 ,
,  , (6)
, (6)
где обозначено
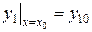 ,
, 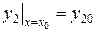 ,
,  ,
,  .
.
Из системы (6) можно определить С1 и С2, так как определитель это системы

есть определитель Вронского при x=x0 и, следовательно, не равен 0 (в силу линейной независимости решений y1 и y2). Частное решение получится из семейства (5) при найденных значениях С1 и С2, удовлетворяет заданным начальным условиям. Таким образом, теорема доказана.
Не существует общих методов для нахождения в конечном виде общего решения линейного уравнения с переменными коэффициентами. Однако для уравнений с постоянными коэффициентами такой метод существует.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1357; Нарушение авторских прав?; Мы поможем в написании вашей работы!