
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Численные методы расчета электромагнитных полей
|
|
|
|
ПРИ СЛОЖНЫХ ГРАНИЧНЫХ УСЛОВИЯХ. СОВРЕМЕННЫЕ ПАКЕТЫ ПРИКЛАДНЫХ ПРОГРАММ РАСЧЕТА ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ НА ЭВМ
ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ
РАСЧЕТ КВАЗИСТАЦИОНАРНОГО ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
С ПОМОЩЬЮ ОБОБЩЕННОГО СКАЛЯРНОГО МАГНИТНОГО ПОТЕНЦИАЛА
Квазистационарные переменные токи характеризуются тем, что в каждый момент времени создают такое же пространственное распределение магнитного поля, как постоянные (стационарные) токи.
Изменяющийся во времени ток распределен внутри проводников по не заданному наперед закону, поэтому для квазистационарного электромагнитного поля функция 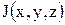 подлежит определению. Принимаем
подлежит определению. Принимаем 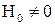 только в объеме, где
только в объеме, где 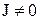 . Тогда в диэлектрике
. Тогда в диэлектрике 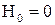 . Сопоставление уравнений
. Сопоставление уравнений 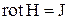 и
и 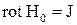 позволяет записать соотношение, связывающее напряженности Н,
позволяет записать соотношение, связывающее напряженности Н,  искомого и вспомогательного полей,
искомого и вспомогательного полей, 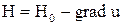 , переходящее в диэлектрике в уравнение
, переходящее в диэлектрике в уравнение 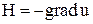 . Для получения уравнения, связывающего
. Для получения уравнения, связывающего  и потенциал u, можно вычислить rot обеих частей соотношения
и потенциал u, можно вычислить rot обеих частей соотношения 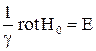 , следующего из уравнения
, следующего из уравнения 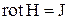 :
:  .
.
Учитывая, что  , находим
, находим 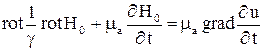 .
.
В это уравнение наряду с  входит и скалярный магнитный потенциал u, для получения уравнения относительно которого используем условие
входит и скалярный магнитный потенциал u, для получения уравнения относительно которого используем условие 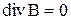 :
:
 ,
,
так что 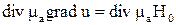 . Обозначая
. Обозначая 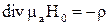 , можно записать, что скалярный магнитный потенциал удовлетворяет внутри проводника уравнению
, можно записать, что скалярный магнитный потенциал удовлетворяет внутри проводника уравнению 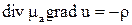 и вне его уравнению
и вне его уравнению 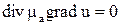 .
.
Таким образом, искомые переменные  , u внутри проводящей среды можно найти, решая систему уравнений
, u внутри проводящей среды можно найти, решая систему уравнений
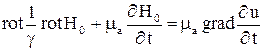 ;
; 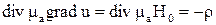 . (1)
. (1)
В точках, где плотность вихревых токов  ,
,
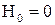 ;
;
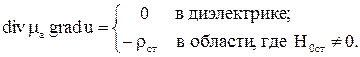
Решив систему (1), можно найти лишь три независимые функции, поскольку ее второе уравнение следует из первого. Поэтому ее можно дополнить условием 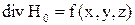 , где
, где 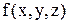 – произвольная функция.
– произвольная функция.
Краевые условия относительно скалярного магнитного потенциала записывают на границе расчетной области, а для функции  – на поверхности проводящего массива. При расчете трехмерного поля, когда плотность J вихревого тока имеет все три составляющие, вектор
– на поверхности проводящего массива. При расчете трехмерного поля, когда плотность J вихревого тока имеет все три составляющие, вектор  также может содержать три составляющие. Тогда функцию
также может содержать три составляющие. Тогда функцию 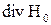 внутри проводящего массива можно выбрать произвольно. Если же принять, что одна из составляющих вектора
внутри проводящего массива можно выбрать произвольно. Если же принять, что одна из составляющих вектора  равна нулю (что возможно даже если J – трехмерный вектор), то функцию
равна нулю (что возможно даже если J – трехмерный вектор), то функцию 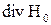 задать произвольно нельзя. Краевые условия для
задать произвольно нельзя. Краевые условия для  в этих двух случаях записываются по-разному. Рассмотрим способы введения вектора
в этих двух случаях записываются по-разному. Рассмотрим способы введения вектора  подробнее.
подробнее.
Случай, когда составляющие  не равны нулю. Выберем функцию
не равны нулю. Выберем функцию 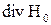 так, чтобы в наибольшей мере упростить вид уравнений системы (1). Учитывая, что
так, чтобы в наибольшей мере упростить вид уравнений системы (1). Учитывая, что 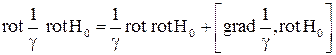 , первое уравнение системы (1) можно записать в виде
, первое уравнение системы (1) можно записать в виде
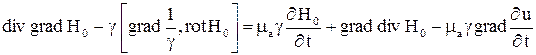 .
.
Если принять  , то для однородного проводящего массива система уравнений (1) преобразуется к виду
, то для однородного проводящего массива система уравнений (1) преобразуется к виду
 ; (2)
; (2)
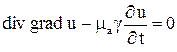 . (3)
. (3)
Уравнения (2), (3) внутри проводящей среды совместно с уравнениями
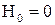 ;
;
 (4)
(4)
вне ее, дополненные граничными и краевыми условиями, образуют
систему, решение которой дает возможность рассчитать электромагнитное поле как внутри, так и вне проводящей среды. Число искомых
скалярных функций равно четырем внутри проводящих массивов
(три составляющие вектора  и скалярный магнитный потенциал
и скалярный магнитный потенциал
u) и одной (потенциал u) вне их. Таким образом, путем введения скалярного магнитного потенциала в области, где плотность вихревого
тока не равна нулю, достигается существенное упрощение задачи,
так как вне объемов с вихревыми токами для расчета поля достаточно
определить скалярный, а не векторный потенциал.
Если отказаться от принятого условия 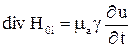 и допустить, что
и допустить, что 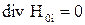 всюду, за исключением точек поверхности проводящего массива, где
всюду, за исключением точек поверхности проводящего массива, где  , то можно упростить задачу определения значений
, то можно упростить задачу определения значений 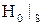 . В этом случае можно принять
. В этом случае можно принять 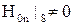 ;
;  и, учитывая
и, учитывая 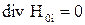 , записать краевое условие для
, записать краевое условие для 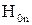 в виде
в виде  . При этом уравнения для переменных
. При этом уравнения для переменных  и u в точках внутри проводника образуют систему
и u в точках внутри проводника образуют систему
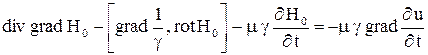 ;
;
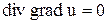
при краевом условии на его поверхности 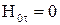 ,
,  .
.
Так как на поверхности проводника 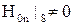 , а вне его
, а вне его 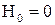 , то это эквивалентно размещению на поверхности проводника простого слоя магнитных зарядов с поверхностной плотностью
, то это эквивалентно размещению на поверхности проводника простого слоя магнитных зарядов с поверхностной плотностью 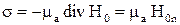 . Нормальная производная скалярного магнитного потенциала имеет на поверхности S разрыв, равный
. Нормальная производная скалярного магнитного потенциала имеет на поверхности S разрыв, равный 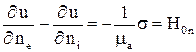 . При таком способе задания функции
. При таком способе задания функции 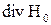 число уравнений внутри проводника равно четырем (для трех составляющих вектора
число уравнений внутри проводника равно четырем (для трех составляющих вектора  и скалярного магнитного потенциала u), но одновременно решение упрощается за счет возможности явного задания краевых условий для
и скалярного магнитного потенциала u), но одновременно решение упрощается за счет возможности явного задания краевых условий для  (
(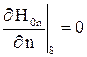 ,
,  ).
).
Число рассчитываемых внутри проводящих массивов скалярных функций можно уменьшить, если принять  и
и
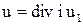 , (5)
, (5)
где i – единичный орт одной из координат;
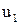 – скалярная функция, подлежащая расчету.
– скалярная функция, подлежащая расчету.
Из (5) 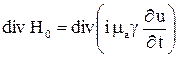 , откуда
, откуда
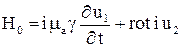 , (6)
, (6)
где 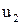 – неизвестная скалярная функция.
– неизвестная скалярная функция.
Если подставить (6) в (2), то можно получить уравнения
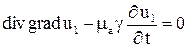 ;
; 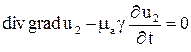 .
.
В результате представления потенциала в виде (5) число искомых скалярных функций, определяемых внутри проводящего массива, можно уменьшить до двух. Переменные 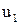 ,
, 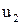 связаны с потенциалом u на поверхности проводящего массива граничными условиями
связаны с потенциалом u на поверхности проводящего массива граничными условиями  ,
,  которые можно записать через переменные u,
которые можно записать через переменные u, 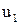 ,
, 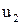 , учитывая, что
, учитывая, что
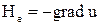 ;
; 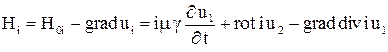 .
.
Введение скалярных функций 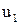 ,
, 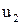 позволяет рассчитать квазистационарное электромагнитное поле с помощью минимально возможного числа уравнений: одного для потенциала вне проводящего массива и двух – для функций
позволяет рассчитать квазистационарное электромагнитное поле с помощью минимально возможного числа уравнений: одного для потенциала вне проводящего массива и двух – для функций 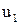 ,
, 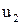 внутри его. Изложенный способ пригоден для решения только тех задач, в которых проводящие массивы однородны. Кроме того, хотя число подлежащих решению уравнений невелико, такой подход требует дополнения уравнений относительно переменных u,
внутри его. Изложенный способ пригоден для решения только тех задач, в которых проводящие массивы однородны. Кроме того, хотя число подлежащих решению уравнений невелико, такой подход требует дополнения уравнений относительно переменных u, 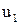 ,
, 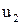 уравнениями, выражающими граничные условия сопряжения. Так как напряженность поля выражается через вторую производную функции
уравнениями, выражающими граничные условия сопряжения. Так как напряженность поля выражается через вторую производную функции 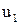 , то и граничное условие сопряжения также содержит слагаемое
, то и граничное условие сопряжения также содержит слагаемое 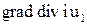 , что усложняет численное решение задачи.
, что усложняет численное решение задачи.
Случай, когда одна из составляющих  равна нулю. В число скалярных функций, которые следует рассчитать в точках внутри проводников, входят скалярный магнитный потенциал и две составляющие вектора
равна нулю. В число скалярных функций, которые следует рассчитать в точках внутри проводников, входят скалярный магнитный потенциал и две составляющие вектора  . Вне объемов с вихревыми токами поле описывается скалярным магнитным потенциалом. Наложенное на вектор
. Вне объемов с вихревыми токами поле описывается скалярным магнитным потенциалом. Наложенное на вектор  ограничение (задание его в виде, обусловливающем равенство нулю одной из его составляющих) не позволяет выбрать произвольной функцию
ограничение (задание его в виде, обусловливающем равенство нулю одной из его составляющих) не позволяет выбрать произвольной функцию 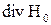 . Поэтому при записи уравнений (1) для
. Поэтому при записи уравнений (1) для  в принятой системе координат функцию
в принятой системе координат функцию 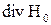 следует выразить в этой системе. Так, в прямоугольной системе координат
следует выразить в этой системе. Так, в прямоугольной системе координат
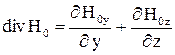 ,
,
если  .
.
Уравнения, которым удовлетворяют искомые составляющие 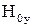 ,
,  следуют из (1):
следуют из (1):
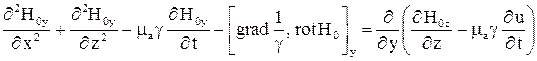 ; (7)
; (7)
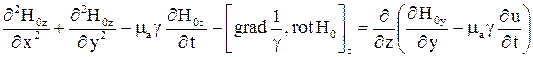 .
.
На поверхности S проводящего массива решается уравнение (1), записанное в проекциях на направления нормали и касательной этой поверхности:
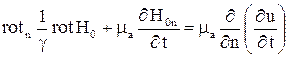 ;
;
 . (8)
. (8)
Граничные условия на поверхности S выполняются, так как любых значениях 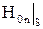 ,
, 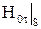 скалярный магнитный потенциал имеет разрыв своей нормальной к S производной (здесь располагается простой слой магнитных зарядов плотностью
скалярный магнитный потенциал имеет разрыв своей нормальной к S производной (здесь располагается простой слой магнитных зарядов плотностью 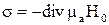 ) и касательной производной
) и касательной производной 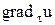 , равной
, равной 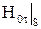 .
.
Для получения единственного решения задачи  может быть задано равным нулю в произвольной точке поверхности проводящего массива. Если
может быть задано равным нулю в произвольной точке поверхности проводящего массива. Если 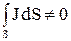 (S – сечение проводника), то в этой точке следует поместить линейный ток
(S – сечение проводника), то в этой точке следует поместить линейный ток 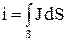 , который можно заменить эквивалентным ему двойным слоем магнитных зарядов.
, который можно заменить эквивалентным ему двойным слоем магнитных зарядов.
Уравнения (7) совместно с уравнением, описывающим скалярный магнитный потенциал, 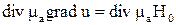 образуют систему, позволяющую рассчитать электромагнитное поле и плотность вихревых токов в проводящем массиве с учетом как анизотропных, так и нелинейных свойств его материала.
образуют систему, позволяющую рассчитать электромагнитное поле и плотность вихревых токов в проводящем массиве с учетом как анизотропных, так и нелинейных свойств его материала.
Рассмотренный метод расчета квазистационарного электромагнитного поля аналогичен методу, основанному на использовании другой пары потенциалов: векторного магнитного А и скалярного электрического  . Применение этих потенциалов приводит к необходимости решения системы уравнений
. Применение этих потенциалов приводит к необходимости решения системы уравнений
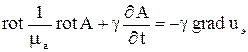 ;
; 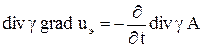
внутри объема с вихревыми токами и системы
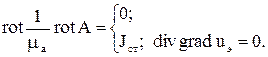
вне этого объема. Учитывая, что на поверхности S массива, исходя из допущения  , где n – нормаль к поверхности S, можно записать
, где n – нормаль к поверхности S, можно записать  , потенциал
, потенциал  определяют только внутри и на поверхности проводника. В соответствии с этим методом внутри проводящего массива расчету подлежат четыре (три составляющие потенциала А и скалярный электрический потенциал
определяют только внутри и на поверхности проводника. В соответствии с этим методом внутри проводящего массива расчету подлежат четыре (три составляющие потенциала А и скалярный электрический потенциал  ), а вне его – три (составляющие потенциала А) скалярные функции. При использовании переменных
), а вне его – три (составляющие потенциала А) скалярные функции. При использовании переменных  и
и 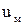 (векторного потенциала тока и скалярного магнитного потенциала) в общем случае необходимо решить уравнения (1) внутри проводящих массивов, т. е. рассчитать также четыре скалярные функции. Однако трудоемкость расчета снижается, во-первых, потому, что в пространстве вне проводящих массивов, используют только скалярный магнитный потенциал и, во-вторых, появляется возможность записи краевого условия для вектора
(векторного потенциала тока и скалярного магнитного потенциала) в общем случае необходимо решить уравнения (1) внутри проводящих массивов, т. е. рассчитать также четыре скалярные функции. Однако трудоемкость расчета снижается, во-первых, потому, что в пространстве вне проводящих массивов, используют только скалярный магнитный потенциал и, во-вторых, появляется возможность записи краевого условия для вектора  в простом виде:
в простом виде: 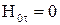 ;
;  . Применение скалярного магнитного потенциала для расчета поля вне проводящих массивов позволяет легко учесть неоднородность сред и нелинейные свойства ферромагнитных материалов, что связано с серьезными трудностями при использовании векторного магнитного потенциала. Преимущества метода могут возрасти еще в большей мере, если для определения поля в проводящих массивах перейти к расчету двух скалярных функций
. Применение скалярного магнитного потенциала для расчета поля вне проводящих массивов позволяет легко учесть неоднородность сред и нелинейные свойства ферромагнитных материалов, что связано с серьезными трудностями при использовании векторного магнитного потенциала. Преимущества метода могут возрасти еще в большей мере, если для определения поля в проводящих массивах перейти к расчету двух скалярных функций 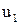 ,
, 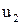 либо двух составляющих вектора
либо двух составляющих вектора  и скалярного магнитного потенциала.
и скалярного магнитного потенциала.
РАСЧЕТ ПЕРЕМННЫХ ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ МЕТОДОМ
КОНЕЧНЫХ ЭЛЕМЕНТОВ
При расчете стационарных и квазистационарных полей известные способы получения уравнений метода конечных элементов приводят к алгебраическим уравнениям одного и того же вида. В то же время применение вариационного подхода к решению уравнений с несимметричными операторами, например, при расчете квазистационарных полей, формально не обосновано так же строго, как использование метода невязок (метода Галеркина). Учитывая, что метод невязок можно применить для получения уравнений не только при расчете стационарных и квазистационарных гармонических, но и переменных полей, целесообразно с единых позиций использовать этот путь получения алгебраических уравнений метода конечных элементов. В соответствии с методом невязок для решения уравнения
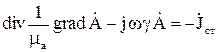
необходимо соблюдать ортогональность базисных функций 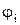 приближенного решения
приближенного решения 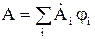 и невязки
и невязки 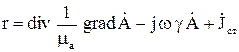 :
:
 (8)
(8)
Для любого значения i интеграл (8) в прямоугольной системе координат можно представить в виде суммы трех интегралов:
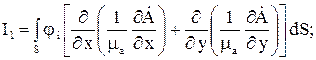 (9)
(9)
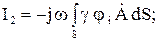 (10)
(10)
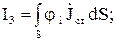 (11)
(11)
Интеграл 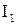 можно преобразовать с помощью формулы Грина:
можно преобразовать с помощью формулы Грина:

 (12)
(12)
Для получения системы алгебраических уравнений относительно узловых переменных 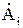 в (9) – (11) следует подставить
в (9) – (11) следует подставить 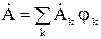 , приравнять к нулю сумму
, приравнять к нулю сумму 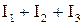 для каждого значения i (
для каждого значения i ( ). С этой целью расчетную область представляют в виде совокупности элементов, площади которых
). С этой целью расчетную область представляют в виде совокупности элементов, площади которых 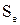 , и записывают интегралы (10) – (12) в виде
, и записывают интегралы (10) – (12) в виде 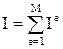 . Нетрудно убедиться в том, что при записи второго интеграла (12) в виде
. Нетрудно убедиться в том, что при записи второго интеграла (12) в виде 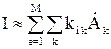 коэффициенты
коэффициенты 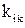 выражают через базисные функции. Интеграл I можно записать в матричной форме
выражают через базисные функции. Интеграл I можно записать в матричной форме  . Интеграл
. Интеграл
 .
.
Для расчета 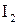 следует подставить
следует подставить 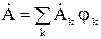 в (10):
в (10):
 ;
;
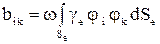 .
.
Если 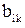 рассматривать как элементы матрицы
рассматривать как элементы матрицы 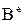 , то можно записать
, то можно записать 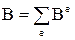 . Тогда
. Тогда 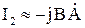 .
.
Первый интеграл в (12) определяется граничным условием второго рода на контуре l расчетной области. Если функция 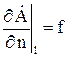 задана, то он не зависит от искомых узловых переменных
задана, то он не зависит от искомых узловых переменных 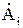 и принимает значение
и принимает значение 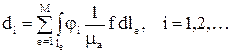 .
.
Коэффициенты  образуют матрицу D:
образуют матрицу D: 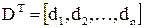 . В тех случаях, когда функция
. В тех случаях, когда функция 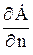 на контуре l неизвестна, интеграл
на контуре l неизвестна, интеграл 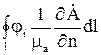 зависит от узловых переменных и его можно представить в виде
зависит от узловых переменных и его можно представить в виде
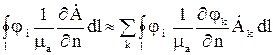 ,
,
если производную 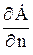 выразить через узловые потенциалы
выразить через узловые потенциалы 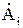 :
: 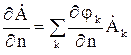 . Уравнения метода Галеркина можно записать, подставив в (8) выраженные через потенциалы
. Уравнения метода Галеркина можно записать, подставив в (8) выраженные через потенциалы 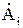 значения интегралов
значения интегралов 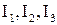 :
:
 ;
;
 , (13)
, (13)
где 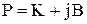 ;
;  .
.
Рассмотрим особенности расчета нестационарного электромагнитного поля методом конечных элементов. Уравнение
 , (14)
, (14)
описывающее процесс проникновения поля в проводящую среду, является уравнением с несимметричным оператором, поэтому при выводе алгебраических уравнений следует использовать метод невязок.
Приближенное решение (14) можно искать в виде
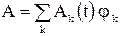 ,
,
где 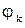 – базисные функции, зависящие от пространственных координат;
– базисные функции, зависящие от пространственных координат;
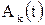 – потенциалы узлов, являющиеся функциями времени.
– потенциалы узлов, являющиеся функциями времени.
В соответствии с методом невязок уравнения относительно искомых значений 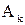 можно записать так:
можно записать так:
 (15)
(15)
Так как оно отличается от рассмотренных ранее наличием слагаемого  , то при замене площади S совокупностью элементов площади
, то при замене площади S совокупностью элементов площади 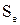 и переходе к алгебраическим уравнениям можно получить те же уравнения, что и при расчете стационарных полей, но дополненные слагаемым, соответствующим последнему интегралу в (15). В результате получаем
и переходе к алгебраическим уравнениям можно получить те же уравнения, что и при расчете стационарных полей, но дополненные слагаемым, соответствующим последнему интегралу в (15). В результате получаем
 .
.
Если ввести матрицы В и 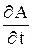 с элементами –
с элементами –  и
и 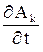 , то система уравнений для узловых переменных примет вид
, то система уравнений для узловых переменных примет вид
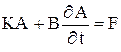 , (16)
, (16)
где К, F – матрицы.
Уравнение (16) записывают относительно 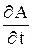 :
:  и решают на совокупности временных слоев.
и решают на совокупности временных слоев.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 2238; Нарушение авторских прав?; Мы поможем в написании вашей работы!