Положительные числовые ряды. Достаточные признаки сходимости

Определение. Числовой ряд (1) называется положительным, если все его слагаемые a_n – положительные числа. Частичная сумма S_n = а₁+ а₂ + …+ а_n такого ряда при любом значении n тоже, естественно, положительна, причем с увеличением номера n она монотонно возрастает. Следовательно, имеются всего две возможности:

1)

2) где S – некоторое положительное число.

В первом случае ряд расходится, во втором сходится. Какая из этих двух возможностей реализуется, зависит, очевидно, от поведения слагаемых 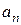ряда при n ® ∞. Если эти слагаемые стремятся к нулю, причем делают это достаточно быстро, то ряд будет сходиться. А если они не стремятся к нулю, или стремятся к нему, но недостаточно быстро, то ряд будет расходиться.

Например, у гармонического ряда (16) слагаемые 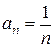хоть и убывают, стремясь к нулю, но делают это довольно медленно. Поэтому гармонический ряд оказался расходящимся. А вот у положительного ряда (6) слагаемые стремятся к нулю гораздо быстрее, поэтому он оказался сходящимся.

Еще пример. Ряд вида

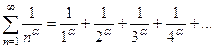(18)

называется обобщенным гармоническим рядом (при 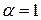это будет обычный гармонический ряд). Если исследовать его на сходимость – расходимость аналогично тому, как исследовался гармонический ряд (16) (с помощью рисунка, подобного рисунку 1), то можно установить (попробуйте это сделать самостоятельно), что обобщенный гармонический ряд расходится при 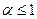(его сумма 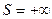) и сходится при (его сумма S – конечное положительное число). И это понятно: при 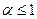слагаемое обобщенного гармонического ряда убывают медленнее слагаемых 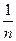гармонического ряда. А так как гармонический ряд расходится (скорость убывания его слагаемых недостаточна для сходимости), то тем более при 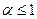будет расходиться и обобщенный гармонический ряд (18). А при слагаемые ряда (18) будут, очевидно, убывать быстрее, чем слагаемые 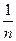гармонического ряда (16). И этой возросшей скорости убывания оказывается достаточно для сходимости ряда (18).

Можно эти соображения изложить строже, в виде так называемого признака сравнения положительных числовых рядов.

Его суть в следующем. Пусть

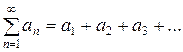(19)

(20)

- два произвольных положительных числовых ряда. И пусть 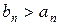для всех n =1,2,…. То есть (20) – ряд с бóльшими членами, чем ряд (19). Тогда очевидно, что:

1) Если ряд с бóльшими членами сходится, то и ряд с меньшими членами сходится.

2) Если ряд с меньшими членами расходится (его сумма равна +∞), то и ряд с бóльшими членами тоже расходится (его сумма тем более равна +∞).

3) Если ряд с бóльшими членами сходится (его сумма равна +∞), то про ряд с меньшими членами ничего сказать нельзя.

4) Если ряд с меньшими членами сходится (его сумма – число), то про ряд с бóльшими членами ничего сказать нельзя.

Замечание 1. В формулировке всех четырех пунктов признака сравнения можно условие 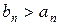, с помощью которого сравниваются ряды и которое должно выполняться для всех n =1,2,3,…, заменить на это же условие 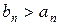, справедливое не для всех n, а лишь начиная с некоторого номера N, то есть для n>N, ибо отбрасывание конечного числа членов ряда не влияет на его сходимость.

В подтверждение сказанного докажем две теоремы.

Теорема 2. Если члены положительного ряда 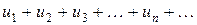(а) не больше соответствующих членов положительного ряда (б), т.е. (*) и ряд (б) сходится, то сходится и ряд (а).

Доказательство. Обозначим через и 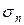, соответственно, частичную сумму первого и второго рядов:

.

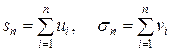Из условия (*) следует, что .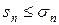

Так как ряд (б) сходится, то существует предел 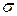его частичной суммы . Из того, что члены рядов (а) и (б) положительны, следует, что 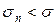, и тогда в силу неравенства 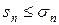, получается .

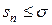Итак, мы доказали, что частичные суммы ограничены. Заметим что при увеличении n частичная сумма возрастает, а из того, что последовательность частичных сумм возрастает и ограничена, следует, что она имеет предел 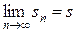, причем очевидно, что .

Теорема 3. Если члены положительного ряда 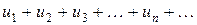(а) не меньше соответствующих членов положительного ряда (б), т.е. (*) и ряд (б) расходится, то расходится и ряд (а).

Доказательство. Из условия (*) следует что 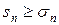. Так как члены ряда (б) положительны, то его частичная сумма 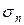возрастает при возрастании n, а так как он расходится, то . Но тогда из неравенства 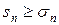следует 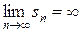, т.е. ряд (а) расходится. Что и требовалось доказать.

Замечание 2. Признак сравнения положительных числовых рядов допускает обобщение. А именно, если существует конечный и отличный от нуля предел

, (21)

то есть если

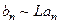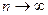при (22)

(b_n эквивалентны La_n при 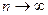), то положительные числовые ряды (19) и (20) сходятся или расходятся одновременно. Данное замечание оставим без доказательства.

Пример 5. Ряд

(23)

расходится (его сумма равна +∞). Действительно, сравнивая этот ряд с гармоническим (16), слагаемые которого меньше слагаемых ряда (23) для всех n >1, сразу приходим к этому выводу на основании пункта 2 признака сравнения. Также его расходимость следует и из того, что это – обобщенный гармонический ряд (18) при .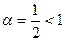

Пример 6. Ряд

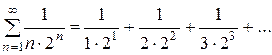(24)

- это положительный ряд с меньшим для всех n >1 слагаемыми, чем ряд

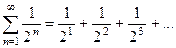(25)

Но ряд (25) представляет собой сумму бесконечной геометрической прогрессии со знаменателем . Такой ряд, согласно (15), сходится и имеет сумму S =1. Но тогда сходится и меньший ряд (24), причем его сумма .

Пример 7. Ряд 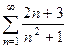- положительный числовой ряд, у которого слагаемые

при .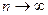

Но ряд 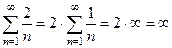расходится в силу (17). Значит, в соответствии с (22), расходится и данный ряд со слагаемыми a_n.

Признак Даламбера. Этот признак состоит в следующем. Пусть - положительный числовой ряд. Найдем предел q отношения последующего члена ряда к предыдущему:

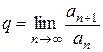(26)

Французский математик и механик 19-го века Даламбер доказал, что при q <1 ряд сходится; при q >1 он расходится; при q =1 вопрос о сходимости - расходимости ряда остается открытым. Доказательство признака Даламбера опускаем.

Пример 8. Исследовать на сходимость – расходимость положительный числовой ряд .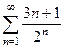

Решение. Применим к этому ряду признак Даламбера. Для этого по формуле (26) вычислим q:

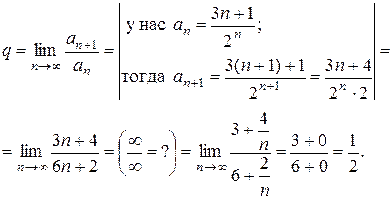
Так как 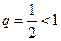, то данный ряд 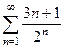сходится.

Радикальный признак Коши. Если для ряда с положительными членами

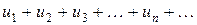
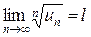величина имеет конечный предел l при , т.е. , то:

1) в случае l<1 ряд сходится;

2) в случае l>1 ряд расходится.

Доказательство признака приводить не будем.

Пример 9. Исследовать на сходимость – расходимость положительный числовой ряд .

Решение. Применим к этому ряду радикальный признак Коши.

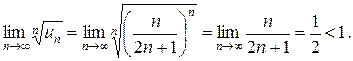
Ряд сходится.

Дата добавления: 2014-01-04