Лекция № 6. Спектральный анализ стационарных случайных процессов

Спектральный анализ стационарных случайных процессов.

6.1 Спектр случайного процесса

Для исследования неслучайных функций весьма широкое применение получил гармонический анализ, то есть разложение функций в виде ряда Фурье, если функции периодические, и в виде интеграла Фурье – если функции непериодические.

Остановимся сначала более подробно на разложении неслучайных функций в ряды по тригонометрическому базису.

Если функция 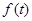имеет период колебаний 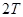, непрерывна и удовлетворяет условиям Дирихле, то ее можно представить в виде комплексного ряда

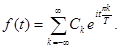, (6.1.1)

где коэффициенты Фурье определяются по формуле

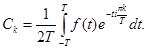(6.1.2)

Формула (6.1.1) позволяет представить функцию 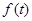в виде бесконечной суммы гармонических колебаний с частотами 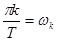и амплитудами 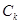, так как известно, что

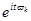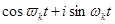= (6.1.3)

Последовательность комплексных чисел 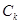спектром функции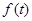. Спектр показывает, какого рода колебания преобладают в данной функции. В данном примере частота колебаний принимает дискретные значения 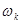, следовательно, функцию 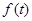называют функцией с дискретным спектром.

Аналогично, если функция непериодическая и существует несобственный интеграл,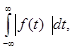то ее можно представить в виде интеграла Фурье

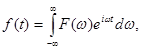(6.1.4)

где

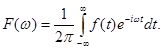(6.1.5)

Формула (6.1.5) будем называть прямым преобразованием Фурье, а формулу (6.1.4) – обратным преобразованием Фурье.

Остановимся на физическом смысле функции 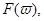которую называют непрерывным спектром или спектральной плотностью функции 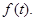Из формул приведенных формул следует, что спектр однозначно определяет функцию и наоборот.

Рассмотрим применение аппарата спектральных разложений к стационарным случайным процессам.

Пусть реализации случайного процесса 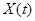, которые являются периодическими функциями с периодом T, представлены в виде гармонических колебаний. Тогда сам случайный процесс, который является их совокупностью, можно представить в виде ряда со случайными амплитудами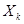

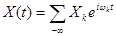, (6.1.6)

где 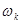- частоты колебаний. Будем считать, что математическое ожидание случайного процесса равно нулю. Тогда корреляционная функция случайного процесса 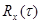можно также представить в виде ряда, в котором коэффициенты разложения представляют собой дисперсии каждого к-го колебания. Иными словами

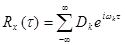. (6.1.7)

Для существования корреляционной функции ряд (6.1.7) должен быть сходящимся, то есть должен сходиться ряд

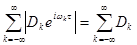(6.1.8)

Мы предположили, что случайный стационарный процесс может быть разложен в ряд (6.1.6), ничем не оговорив условия этого разложения. При этом получили, что корреляционная функция определяется в виде ряда (6.1.7), а случайные амплитуды - взаимно некоррелированные случайные величины.

Советский математик Е.Е.Слуцкий доказал теорему, что всякий стационарный случайный процесс, имеющий корреляционную функцию (6.1.7), может быть представлен в виде ряда (6.1.6). Для такого ССП спектром называется распределение дисперсий по частотам . Дисперсию случайного процесса получим, положив в формуле (6.1.7) 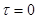. При этом

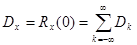(6.1.9)

Следовательно, дисперсия случайного процесса равна сумме ряда, составленного из всех ординат спектра.

На рис.6.1. представлен спектр случайного процесса.

--------------------------------------------------------------------------

Рис.6.1.

По оси абсцисс отложены значения частот, а по оси ординат – соответствующие им дисперсии.

6.2. Спектральная плотность ССП

Рассмотрим теперь ССП, заданный на всей вещественной оси. Для определения корреляционной функции в этом случае осуществим в формуле (6.1.7) предельный переход. Это равносильно бесконечному уменьшению интервала между частотами

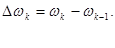
Если обозначить через 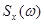среднюю плотность дисперсии в диапазоне частот , то корреляционную функцию можно записать в виде интеграла

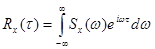. (6.2.1)

Функция 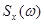называется спектральной плотностью стационарного случайного процесса 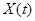. Она представляет собой плотность дисперсии случайного процесса при данной частоте 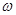. Прямым преобразованием Фурье можно получить формулу для ее определения:

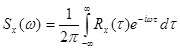(6.2.2)

Так как спектральная плотность является неотрицательной функцией, то корреляционной функцией ССП может служить только функция, преобразование Фурье которой является неотрицательной функцией при всех значениях частоты .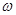

А. Я. Хинчин показал, что и каждая функция, являющаяся обратным преобразованием Фурье от неотрицательной функции, является корреляционной функцией некоторого стационарного случайного процесса.

Полагая в формуле (6.2.1) 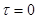, получим выражение для дисперсии случайной функции

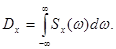(6.2.3)

Можно рассматривать и нормированную спектральную плотность 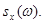ЕЕ можно получить по формуле

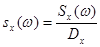(6.2.4.)

Дата добавления: 2014-01-04