Закон полного тока для магнитного поля в веществе. Напряженность магнитного поля

Постановка задачи. В пространство, окружающее макротоки 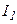, 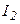…(рис. 24.2) вносим различного рода магнетики, которые в поле токов 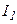,…будучи намагничиваться. Найдем связь напряженности магнитного поля с токами. Предварительно свяжем намагниченность 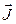с молекулярными токами. Обозначим алгебраическую сумму макротоков 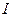, алгебраическую сумму микротоков .

Рассмотрим элемент контура 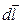(рис. 24.3). Токи молекул справа (вне контура) не пронизывают контур. Слева (внутри контура) пронизывают контур дважды и вклад в алгебраическую сумму токов равен нулю.

Рис. 24.2

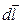Дают вклад только те токи, которые «нанизаны» на контур. Элемент контура , образующий с направлением намагниченности 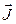угол , нанизывает на себя те молекулярные токи, центры которых попадают внутрь косого цилиндра с объемом (– площадь, охватываемая отдельным молекулярным током, – высота косого цилиндра). Обозначим через 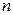концентрацию токов 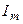в единице объема. Сумма молекулярных токов в элементарном объеме :

.

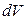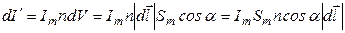Произведение 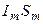равно магнитному моменту отдельного молекулярного тока 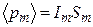, в свою очередь 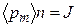, следовательно:

(по определению скалярного произведения). Проинтегрируем по контуру :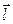

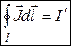
Циркуляция вектора 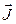по контуру 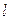равна алгебраической сумме молекулярных токов , натянутых на этот контур.

Закон полного тока с учетом токов проводимости и молекулярных токов: 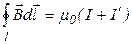, где – алгебраическая сумма макротоков (знак «+» или «-» берется в соответствии с правилом правого винта по отношению к направлению обхода контура).

Раскроем скобки и заменим на :

Поделив обе части на и перенося в левую часть, получим:

.

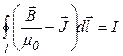Обозначим

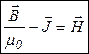
где 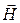– напряженность магнитного поля. Эта величина не имеет особого физического смысла, но приносит пользу. С учетом введенного понятия напряженности получаем теорему о циркуляции вектора 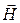(закон полного тока для магнитного поля в веществе):

Циркуляция вектора напряженности магнитного поля по некоторому контуру равна алгебраической сумме макротоков, охватываемых этим контуром.

Таким образом, используя в расчетах вектор 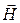можно не учитывать молекулярные токи.

Дата добавления: 2014-01-04