
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Расчетные соотношения для выпрямителей с активно- емкостной нагрузкой
|
|
|
|
Для получения удобных для применения на практике соотношений при анализе выпрямителей с активно-емкостной нагрузкой приняты следующие допущения и упрощения:
-диод будем считать идеальным (Е0 = 0; Iобр = 0);
-конденсатор С имеет достаточно большую ёмкость, так что напряжение на нем постоянно и равно U0;
-напряжение на вторичной обмотке трансформатора изменяется по закону косинуса:
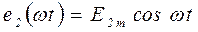 .
.
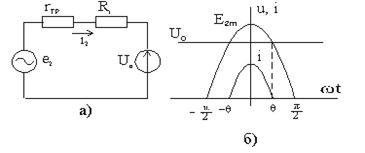
С учетом этого эквивалентная схема для проводящего состояния диода имеет вид, показанный на рис.1.7а (заряженный конденсатор по теореме компенсации заменен источником напряжения U0).
График тока в цепи показан на рис.1.7б.
Согласно закону Ома:
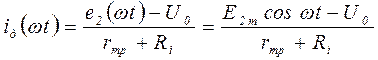 .
.
Это выражение справедливо при 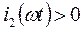 , что имеет место при
, что имеет место при
 |
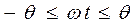 , где
, где 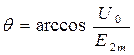 .
.
Рис. 1.7.Схема замещения выпрямителя для проводящего состояния диода (а) и график тока диода (б)
Среднее значение тока диода для однополупериодной схемы является током нагрузки, для двухполупериодной – половиной тока нагрузки. Для получения общей формулы введём коэффициент р - число зарядных импульсов конденсатора С за период напряжения сети. Для однополупериодной схемы р = 1, для двухполупериодной р = 2.
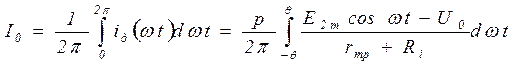 .
.
Согласно рис.1.7б 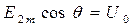 .
.
Обозначим 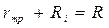 - сопротивление, ограничивающее заряд конденсатора С. С учетом этих обозначений:
- сопротивление, ограничивающее заряд конденсатора С. С учетом этих обозначений:
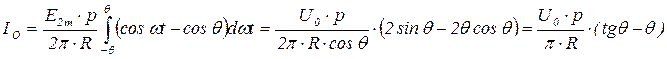
Выражение 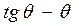 определяется через параметры выпрямителя и называется первым расчетным параметром выпрямителя А:
определяется через параметры выпрямителя и называется первым расчетным параметром выпрямителя А:
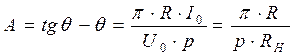 .
.
Так как уравнение 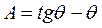 не решается, то определение угла отсечки
не решается, то определение угла отсечки 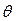 производится по графической зависимости
производится по графической зависимости 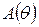 .
.
Из выражения 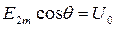 можно определить действующее значение напряжения на вторичной обмотке трансформатора Е2 (в режиме холостого хода):
можно определить действующее значение напряжения на вторичной обмотке трансформатора Е2 (в режиме холостого хода):
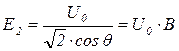 , где
, где 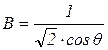 .
.
Для определения мощности силового трансформатора необходимо определить действующее значение тока вторичной обмотки трансформатора. Вначале определим действующее значение тока диода или действующее значение тока за половину периода:
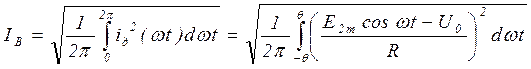 .
.
После подстановок 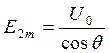 и
и 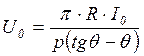 и выполнения интегрирования получим:
и выполнения интегрирования получим:
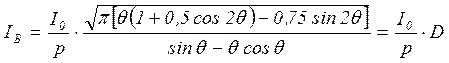 , где D является функцией угла отсечки
, где D является функцией угла отсечки 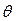 .
.
Для однополупериодной схемы и схемы со средней точкой ток вторичной обмотки трансформатора и ток диода совпадают по форме, поэтому для этих схем I2 = IВ. Для мостовой схемы выпрямителя через вторичную обмотку протекают токи обеих пар диодов, поэтому:
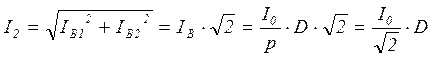 .
.
Ток первичной обмотки трансформатора для однополупериодной схемы определяется с учетом того, что постоянная составляющая тока вторичной обмотки не трансформируется в первичную:
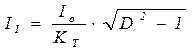 .
.
Для двухполупериодных схем ток первичной обмотки равен:
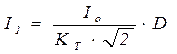 .
.
В выпрямителях с активно-емкостной нагрузкой ток диода имеет импульсный характер. Вследствие достаточно большой длительности импульса амплитудное значение тока диода не должно превышать допустимое прямое значение тока более чем в 4-5 раз. Поэтому в выпрямителях с активно-емкостной нагрузкой необходимо проверять выполнение этого условия.
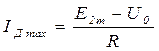 ,
,
и с учетом аналогичных подстановок получим:
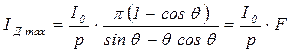 ,
,
где F является функцией угла отсечки 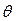 .
.
В реальных условиях конденсатор С имеет конечную ёмкость, т.е. конкретное значение сопротивления конденсатора основной гармонике напряжения на конденсаторе. Падение напряжения на этом сопротивлении определяет пульсации выходного напряжения выпрямителя.
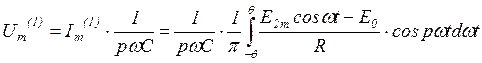 .
.
После подстановок и интегрирования получаем выражение:
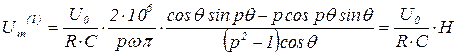 .
.
Расчетный параметр Н является функцией не только угла отсечки 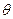 , но и числа зарядных импульсов конденсатора р, и частоты сети
, но и числа зарядных импульсов конденсатора р, и частоты сети 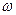 .
.
Коэффициент пульсаций напряжения на нагрузке:
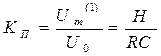 .
.
Все полученные расчетные параметры A, B, D, F, H являются функциями угла отсечки 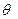 , поэтому на практике приводятся зависимости параметров B, D, F, H от А: B(A), D(A),F(A),H(A;p;w) (рис.1.8).
, поэтому на практике приводятся зависимости параметров B, D, F, H от А: B(A), D(A),F(A),H(A;p;w) (рис.1.8). 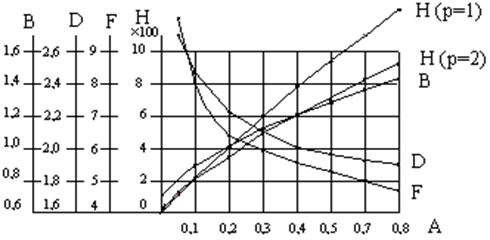
Рис. 1.8. Зависимости расчетных параметров выпрямителя от параметра А
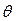 0 0
| ||||||||
| A | 0.05 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 |
| B | 0.82 | 0.91 | 1.03 | 1.12 | 1.21 | 1.28 | 1.36 | 1.43 |
| D | 2.7 | 2.46 | 2.22 | 2.1 | 2.02 | 1.97 | 1.93 | 1.9 |
| F | 6.4 | 5.9 | 5.6 | 5.3 | 5.0 | 4.7 | ||
| H (1) | ||||||||
| H (2) |
Вследствие зависимости параметров выпрямленного напряжения от угла отсечки 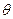 нагрузочная характеристика выпрямителя с активно-емкостной нагрузкой не является линейной. Общий вид нагрузочной характеристики определяется углом отсечки, поэтому целесообразно пользоваться нагрузочной характеристикой в координатах, являющихся функциями угла отсечки
нагрузочная характеристика выпрямителя с активно-емкостной нагрузкой не является линейной. Общий вид нагрузочной характеристики определяется углом отсечки, поэтому целесообразно пользоваться нагрузочной характеристикой в координатах, являющихся функциями угла отсечки 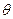 . Эти координаты получаются из ранее полученных соотношений для выпрямителя с активно-емкостной нагрузкой. Напряжение на нагрузке U0 равно:
. Эти координаты получаются из ранее полученных соотношений для выпрямителя с активно-емкостной нагрузкой. Напряжение на нагрузке U0 равно:
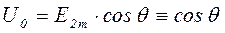 .
.
Ток нагрузки I0 равен:
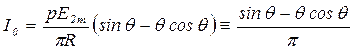
или:
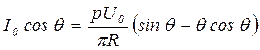 ,
,
отсюда
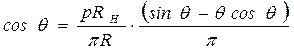 .
.
Зависимость 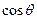 от выражения
от выражения 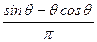 является обобщенной нагрузочной характеристикой (рис.1.9). Для получения реальной нагрузочной характеристики значение ординаты умножается на E2m, а значение абсциссы умножается на сомножитель
является обобщенной нагрузочной характеристикой (рис.1.9). Для получения реальной нагрузочной характеристики значение ординаты умножается на E2m, а значение абсциссы умножается на сомножитель 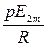 .
.
Реальная нагрузочная характеристика представляется в координатах  ,
, 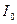 .
.
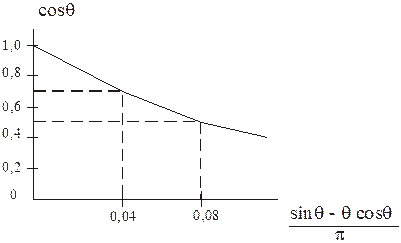
Рис. 1.9. Нагрузочная характеристика выпрямителя с активно-емкостной нагрузкой
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1107; Нарушение авторских прав?; Мы поможем в написании вашей работы!