Определение кромок

Предварительная обработка информации

Лекция № 19

Определение кромок основано на вычислении первых и вторых производных. Так как координаты две - x и y, то это частные производные.

Поскольку первая производная для 2-х координат получается из величины градиента, то отсюда и первое название метода - вычисление градиента, а поскольку вторая производная определяется с помощью преобразования Лапласа, то второе название этого метода - определение оператора Лапласа.

Но это всё один метод определения кромки, основанный на 2-х подходах.

Их суть определим на идеализированном примере:

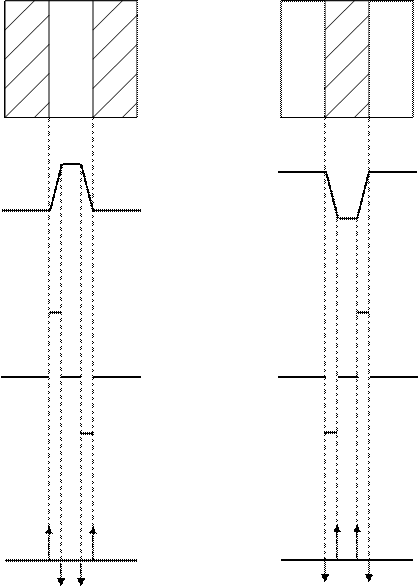а) б)

Изображение

Кривая интен-

сивности по

горизонтальной

линии

Первая

производная

Вторая

производная

Рис.1: Определение кромок с помощью производных. а) – светлый объект на темном фоне, б) – темный объект на светлом фоне.

Вычисление градиента: Градиент изображенияf (x, y) в точке (x, y) определяется как двумерный вектор:

Y grad f = f `(x, y) = G [f(x, y)] = =

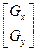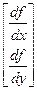
= f

X

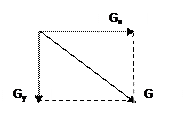Вычисление градиента:

Модуль градиента:

На практике, как правило, градиент аппроксимируют абсолютными значениями:

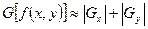
Такая аппроксимация значительно упрощает реализацию метода

Переходим к дискретному представлению G[f(x, y)]

,

.

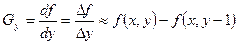Если брать окрестность 3×3, то (1)

(2)

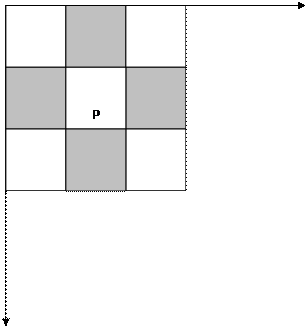
Выражения (1) и (2) первоначально можно записать через координаты пикселей в окрестности f (x, y):

х

х

a	b	c
d	f (x, y)	e
g	h	i

=

=

Тогда маски для вычисления grad f:

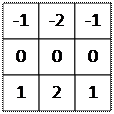G_x G_y

Эти две маски обычно называют операторами Собеля.

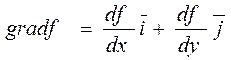= G_x + G_y = G[f (x, y)] (*)

Оператор Лапласа:

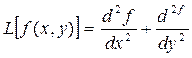
Маска для вычисления оператора Лапласа,

a	b	c
d	f (x, y)	e
g	h	i

т.е.

? Когда градиенты, вычисленные по Собелю и по Лапласу, дадут нули.

Все маски дают «0» на участках постоянной интенсивности изображения, а маска Лапласа также на участках с не изменяющейся интенсивностью на кромках.

Дата добавления: 2014-01-04