Симметричные составляющие несимметричных трехфазных систем

В границах линейных соотношений в электрических цепях любую несимметричную систему: напряжений, ЭДС, токов, магнитных потоков и т.д. можно представить тремя симметричными системами: прямой, обратной и нулевой последовательностями чередования фаз. Такое представление позволяет задачу анализа несимметричного режима работы цепи в условиях влияния сопротивлений фаз друг на друга, когда неприменим принцип взаимности, свести к рассмотрению, в общем случае, трех более простых симметричных режимов, определяемых каждой симметричной составляющей; характеристики несимметричного режима определяются суммированием соответствующих характеристик симметричных.

Основные положения метода представления несимметричной системы симметричными составляющими рассмотрим на примере несимметричной системы фазных напряжений (рис. 7.28).

В соответствии с этим методом векторы симметричных составляющих будут записаны в виде следующих векторов:

1) векторы, составляющие прямую последовательность чередования фаз

;

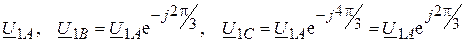2) векторы, составляющие обратную последовательность чередования фаз

;

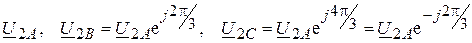3) векторы, составляющие нулевую последовательность чередования фаз

.

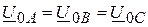Фазовый множитель 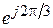называется оператором поворота и обозначается буквой a:

.

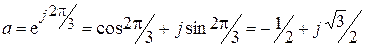Умножение любого вектора на оператор поворота соответствует повороту этого вектора на 120° против часовой стрелки

.

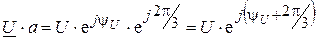Если возвести оператор поворота в квадрат, то получим

.

Отсюда следует, что умножение вектора на a ² соответствует его повороту на 120° по часовой стрелке.

Можно показать, что

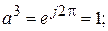
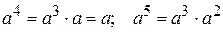и т.д.

Величины 1, a, a ² образуют симметричную систему единичных векторов. Их сумма будет равна

,

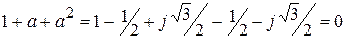а разность операторов поворота

.

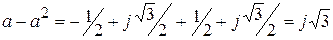С учетом введенного понятия о фазовом множителе и связанных с ним соотношений векторы прямой обратной и нулевой последовательностей фаз запишутся:

прямая последовательность – ;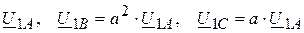

обратная последовательность – ;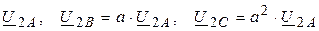

нулевая последовательность – .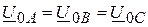

Векторы исходной несимметричной системы представляются в виде геометрической суммы векторов симметричных составляющих:

;

;

.

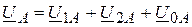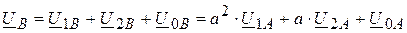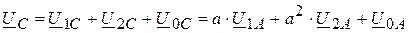Если для упрощения опустить индекс A в правой части, то получим

;

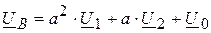; (7.9)

.

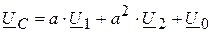Здесь U ₁, U ₂, U ₀ – векторы напряжений прямой, обратной и нулевой последовательностей фазы A. Их называют опорными векторами симметричных составляющих. Если решить последнюю систему уравнений относительно неизвестных опорных векторов при известных фазных напряжениях исходной несимметричной системы, то получим

;

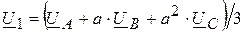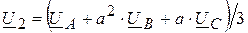; (7.10)

.

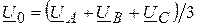Выражения (7.9) и (7.10) позволяют решить задачу определения векторов несимметричной системы по известным симметричным составляющим и наоборот – по известным векторам исходной системы находить опорные векторы симметричных составляющих.

Дата добавления: 2014-01-04