Разряд конденсатора на цепь RL

Расчет переходного процесса классическим методом

ЛЕКЦИЯ №28

ПРОГРАММНЫЕ ТЕРМОРЕГУЛЯТОРЫ

ИСПОЛНИТЕЛЬНЫЕ МЕХАНИЗМЫ

Для перемещения органов управления в системах автоматического регу­лирования служат исполнительные механизмы. Они могут быть электриче­скими, пневматическими и гидравлическими.

К электрическим исполнительным механизмам для позиционного регули­рования относятся: 1) контакторы и магнитные пускатели, включающие и отключающие цепи питания электрических печей; 2) электромагнитные приводы — соленоидные клапаны и 3) электромоторные приводы, состоящие из электродвигателя, редуктора и путевых выключателей. В пневматических исполнительных механизмах мембранного типа мембрана соединена непосред­ственно с регулирующим клапаном. Гидравлические исполнительные меха­низмы представляют собой поршневые сервомоторы. Они могут быть с криво­шипным механизмом и прямого хода.

В некоторых сложных процессах термической обработки подъем темпера­туры, выдержка и снижение температуры должны совершаться через опре­деленные интервалы времени. Для таких процессов необходимо применять программное регулирование, т. е. регулирование процесса по заранее уста­новленному режиму. Это осуществляется специальными приборами, которые называются программными терморегуляторами. Они представляют собой потенциометры обычного типа с дополнительным устройством в виде копира, по которому проходит кулачок или щуп, связанный с органами включения и выключения электрической энергии или подачи топлива.

В качестве примера рассмотрим расчет переходного процесса классическим методом для схемы, изображенной на рис. 9.13. Определить ток .

	Рис. 9.13. Расчетная схема

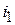1. Для цепи после коммутации составляются уравнения по I и II законам Кирхгофа.

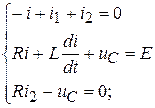
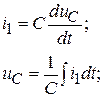
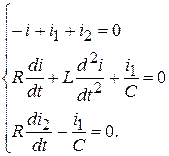
2. Определяются независимые начальные условия 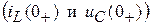из расчета схемы до коммутации:

;

.

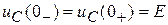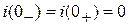3. Искомая величина записывается в виде

.

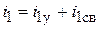4. Установившуюся составляющую определяют из расчета режима цепи после коммутации 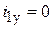(при E = const ток после коммутации есть ток во внешнем контуре).

5. Составляется характеристическое уравнение, и определяются его корни

.

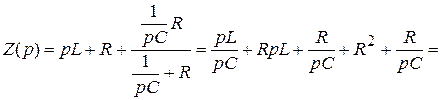
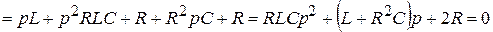Корни могут быть:

1) действительные разные p ₁ и p ₂;

2) действительные равные p ₁ = p ₂ = p;

3) комплексно сопряженные ,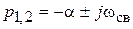

где a – коэффициент затухания;

w_св – угловая частота свободных колебаний.

6. В соответствии с полученными корнями характеристического урав­нения записывается свободная составляющая:

1) ;

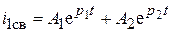2) ;

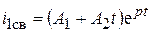3) 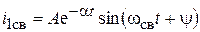, где .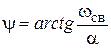

7. Искомое решение для первого случая

.

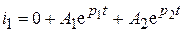8. Определяются постоянные интегрирования A ₁ и A ₂:

,

.

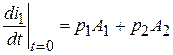Уравнения п.1 для момента времени t = 0 запишутся как

.

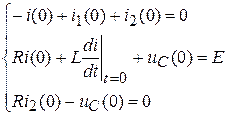Независимые начальные условия i (0) и 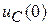уже определены в п.2. Зависимые начальные условия i ₁(0), i ₂(0) и 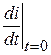определяются из последней системы уравнений.

Для определения 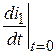необходимо продифференцировать систему уравнений п.1:

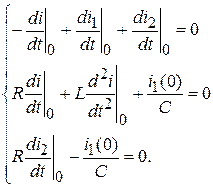
9. После определения постоянных интегрирования A ₁ и A ₂ подставляют их в искомое решение и расчет окончен.

Для определения других токов и напряжений не требуется выполнять все этапы расчета. Можно использовать известные выражения

.

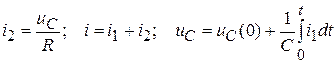В этом случае приложенное напряжение, а также ток установившегося режима равны нулю:

.

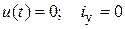Для определения произвольных постоянных интегрирования в уравнении (9.38) необходимо положить: .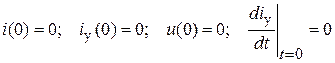

		Рис. 9.14. Расчетная схема

Обозначим 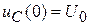. Тогда

.

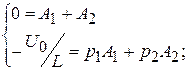
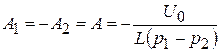Переходный ток

. (9.39)

Напряжения на катушке и конденсаторе

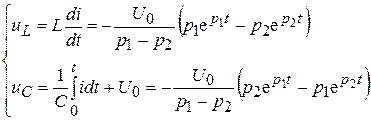. (9.40)

При выводе последнего уравнения учитывалось, что .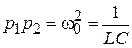

Характер процессов при разряде конденсатора оказывается различным в зависимости от того, будут ли корни характеристического уравнения вещественными или комплексными, что определяется соотношениями между параметрами R, L и C.

Рассмотрим возможные случаи.

1. Пусть корни характеристического уравнения вещественны и отличны друг от друга. Это имеет место при условии

.

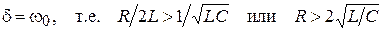Так как 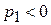и 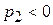и, кроме того, 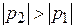, то при изменении t от 0 до ¥ величины 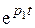и 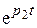убывают от 1 до 0 и при том разность 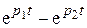всегда положительна (рис. 9.13).

Ток i не меняет своего направления, т.е. конденсатор все время разряжается. Такой односторонний разряд конденсатора называют апериодическим. Кривые изменения напряжений показаны на рис. 9.14.

В интервале времени 0 < t < t_m ток по абсолютному значению возрастает и достигает максимума при 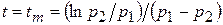. Значение t_m находится из условия 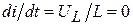. В интервале времени t_m < t < ¥ ток по абсолютному значению убывает, стремясь к нулю.

1. Рассмотрим случай, когда корни характеристического уравнения ве­щест­венны и равны друг другу.

Рис. 9.14. Кривые изменения тока и напряжений на элементах при апериодическом разряде

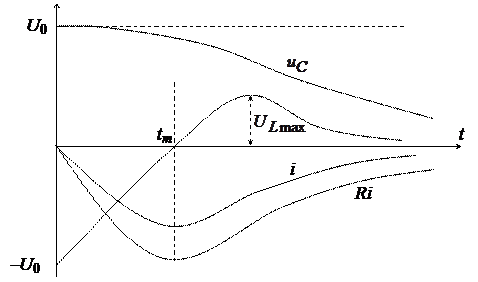Это происходит при 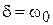, т.е. при 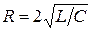. В этом случае 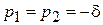. При этом выражения для тока и напряжения (9.39) и (9.40) становятся неопределенными из-за равенства нулю числителя и знаменателя. Раскроем эти неопределенности по правилу Лопиталя, считая, что p ₁ – переменная и стремится к 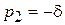. Для тока получим

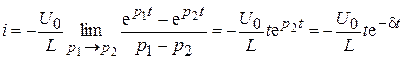. (9.41)

Для напряжений

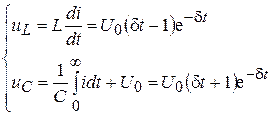. (9.42)

Характер процесса здесь также апериодический. Момент достижения током максимума абсолютного значения равен 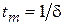. Данный случай при 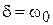является предельным случаем апериодического разряда.

3. Пусть корни характеристического уравнения являются комплексными. Это имеет место при условии 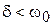, т.е. при 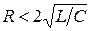. Обозначим 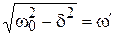. Тогда корни характеристического уравнения запишутся:

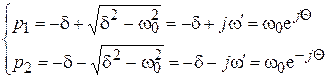, (9.43)

где 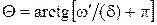. Угол Q лежит в пределах 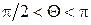, так как 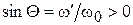и .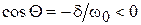

Переходный ток

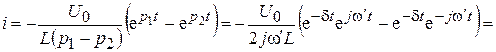
. (9.44)

Уравнения для напряжений

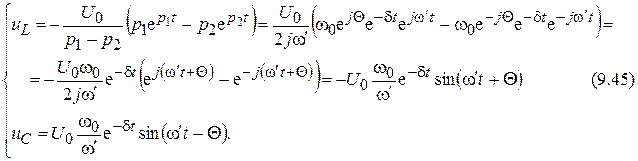
На рис. 9.15 показаны кривые колебательного разряда конденсатора.

Кривая тока i подобна кривой Ri. Процесс в данном случае является колебательным. Ток и напряжение на всех участках периодически меняют знак. Амплитуда колебаний убывает по экспоненциальному закону, в цепи совершаются затухающие колебания. Угловая частота этих колебаний

.

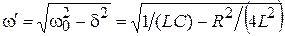В предельном случае R = 0 имеем d =0 и 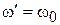, . В этом случае колебания будут незатухающими. Период незатухающих колебаний и угловая частота этих колебаний:

Следовательно, 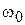равна резонансной частоте контура.

Быстроту затухания тока принято характеризовать декрементом колебаний: . (9.46)

Логарифмический декремент колебаний

. (9.47)

При малом затухании

,

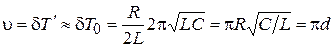где d – затухание контура.

Дата добавления: 2014-01-04