Решение уравнений численными методами

Для решения линейных и нелинейных алгебраических уравнений в SMath Studio используется функция solve, которая представлена в двух вариантах - solve(2) и solve(4) (рис. 8).

Рис. 8

После записи данной функции на листе программы достаточно, не убирая с уравнения курсор, выполнить действие численного вычисления (кнопка "=" на клавиатуре или на панели программы). Само уравнение, записанное в качестве первого аргумента функции solve(...),может быть записано без правой части (т.е., к примеру: "x+2") или вместе с ней ("x+2=0"). Однако следует помнить, что в случае записи уравнения в полном виде (с правой частью), необходимо вместо обычного знака "=" между левой и правой частями уравнения вставлять знак булево равно (выглядит, как жирное равно).

Пример решения уравнения (4) для обоих вариантов функции solve показан на рис. 9.

Рис. 9

В математическом пакете SMath Studio найти решение уравнения можно при помощи стандартной функции roots (рис. 10).

Рис. 10

В данной функции реализован метод Ньютона для нахождения корней уравнения, поэтому необходимо задавать начальное значение x, с которого и начинается поиск корня. Чтобы решить уравнение с помощью данной функции надо выполнить следующую последовательность действий:

- задать произвольное, начальное значение аргумента, неизвестной переменной решаемого уравнения;

- сообщить вид функции f(x):=…;

- задать функцию root по схеме root(f(x),x);

- попросить вывести значение результата root(f(x),x)=…..

Примечания.

1. Функция roots определяет только один корень уравнения. Если в уравнении несколько корней, то определяется тот, к которому ближе всего заданное начальное значение переменной.

2. Функции roots можно не давать ни какого идентификатора, но поставить знак «равно» сразу после нее – компьютер сообщит значение найденного корня.

3. Очень часто при введении функционального идентификатора f(x) в функцию roots результат не получается. В этом случае вместо идентификатора f(x) следует в функции roots напечатать вид самого уравнения, точнее его левой части. Например. roots(x²-6x+5;x)

Варианты решения уравнения (5) с помощью функции roots(2) показаны на рис. 11.

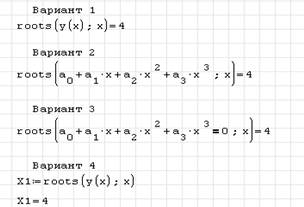
Рис. 11

Три первых варианта демонстрируют разные способы записи первого аргумента функции roots. Вариант 4 демонстрирует возможность присвоения функции roots своего идентификатора, тогда под этим идентификатором и сохранится найденное значение корня. Например, X1:=roots(f(x);x), далее можно вывести значение этого идентификатора X1=4.

Поиск корней уравнения (5) с помощью функции roots(3) (рис. 10) путем изменения их приближенных значений показаны на рис. 12.

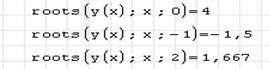
Рис. 12

Приближенные значения корней могут быть известны из физического смысла задачи, из решения аналогичной задачи при других исходных данных, из решения задачи графическим методом.

Из рис. 12 следует, что из трех корней уравнения (5) функция roots(2) определяет только один корень. Для выражения y(x) с известным корнем а нахождение дополнительных корней y(x) эквивалентно поиску корней уравнения h(x) = y(x)/(x - a). Подобный прием полезен для нахождения корней, расположенных близко друг к другу. Проще искать корень выражения h(x), чем пробовать искать другой корень уравнения y(x) = 0, выбирая различные начальные приближения.

Поиск всех корней уравнения (5) с помощью вышеуказанного способа показан на рис. 13.

Рис. 13

Если функция y(x) имеет малый наклон около искомого корня, то функция roots может сходиться к значению x, отстоящему от корня достаточно далеко. В таких случаях для нахождения более точного значения корня следует заменить уравнение y(x) = 0 на z(x) = 0:

z(x)=y(x)/(dy(x)/dx).

В некоторых случаях может отсутствовать сходимость функции roots. Эта ошибка может быть вызвана следующими причинами:

· уравнение не имеет корней.

· корни уравнения расположены далеко от начального приближения.

· выражение имеет локальные экстремумы между начальным приближением и корнями.

· выражение имеет разрывы между начальными приближениями и корнями.

· выражение имеет комплексный корень, но начальное приближение было вещественным.

Чтобы установить причину ошибки, исследуйте график y(x). Он поможет выяснить наличие корней уравнения y(x) = 0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее будет roots сходиться.

Задания 5,6. Выполнить решение всех примеров данного раздела, а также решить уравнения в соответствии с заданным вариантом.

Дата добавления: 2014-01-04