
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Функции комплексного переменного и элементы высшей алгебры
|
|
|
|
§ 1 Комплексные числа и действия над ними
1.1 Понятие мнимой единицы и комплексные числа
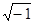 = i – мнимая единица
= i – мнимая единица
bi– мнимые числа, где b = const ≠ 0
Применение мнимой единицы
С помощью мнимой единицы можно извлечь корни четной степени из отрицательного числа
Пример: 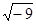 =
= 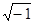
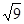 = ±3
= ±3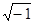 = ±3
= ±3
Комплексным числом называется составное (сложное) число z = a + bi, где а – действительная часть, а b – мнимая.
Re Z = a – действительная часть
Im Z = b – мнимая часть
Z = a + bi -алгебраическая формула комплексного числа
Множество комплексных чисел – это объединение множества действительных и мнимых чисел.
§ 1.2 Степени мнимой единиццы
i¹ = i
i ² = - 1
i ³ = i²·i = -1i = -i
i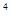 = i²·i² = -1·(-1) = 1
= i²·i² = -1·(-1) = 1
i 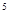 = i
= i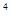 ·i = 1i = i
·i = 1i = i
i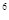 = i
= i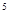 ·i = i·i = i² = -1
·i = i·i = i² = -1
i  = i
= i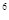 ·i = -1·i = -i
·i = -1·i = -i
i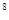 = i
= i ·i = -i·i = (-i)² = -1·(-1) =1
·i = -i·i = (-i)² = -1·(-1) =1
Видно, что степень мнимой единицы принимает всего четыре различных значения, поэтому при вычислении степени мнимой единицы юудем из показателя степни выбрасывать числа, кратные 4.
§ 1.3 Сложение и вычитание комплексных чисел.

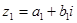 z
z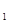 +z
+z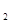 =?
=?
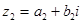
z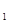 +z
+z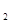 = (
= (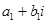 ) + (
) + (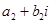 ) =
) = 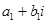 +
+ 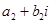 = (
= (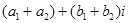
Правило: для того, чтобы сложить два комплексных числав алгебраической форме, нужно сложить их действительные части и коэффициенты при мнимых единицах. Правило справедливо для любого числа слагаемых

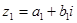
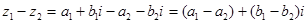
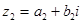
Правило: для того, чтобы из одного комплексного числа вычесть другое комплексное число в алгебраической форме, можно найти разность их действительных частей и разность коэффициентов при мнимой единице.
§ 1.4 Умножение и деление комплексных чисел

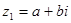
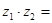 (
(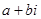 )(
)(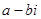 )=
)= 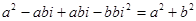
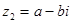
Правило: при умножении двух комплексных чисел в алгебраической форме, нужно раскрыть скобки, т.е. выполнить умножение многочлена на многочлен, привести подобные и заменить i² на – 1. Можно умножать и несколько комплексных чисел.
Два комплексных числа называюься сопряженными, если они отличаются друг от друга только знаком мнимой части.

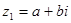
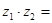 (
(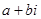 )(
)(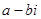 ) =
) = 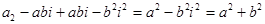
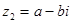
Правило: произведение двух сопряженных чисел представляет собой сумму квадратов их действительной части и коэффициентов при мнимой единице.
Применение: можно разложить сумму квадратов на 2 множителя.
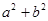 =(
=(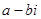 )(
)(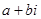 )
)

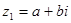
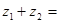 0
0
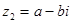
 Правило: при делении двух комплексных чисел, знаменатель преобразуют таким образом, чтобы получить действительное число, т.е. домножают на сопряженное.
Правило: при делении двух комплексных чисел, знаменатель преобразуют таким образом, чтобы получить действительное число, т.е. домножают на сопряженное.
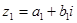
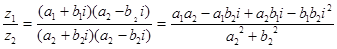
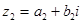
=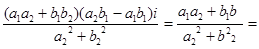
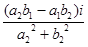
Re 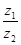 =
=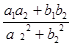
Im 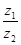 =
=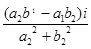
I
§ 1.5 Законы, которые имеют место для всех рассмотренных действий.
1. Коммутативный (переместительный)
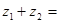
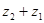
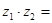
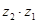
2. Ассоциотивный
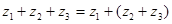
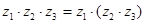
3. Дистрибутивный
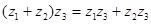
§ 1.6 Геометрическая интерпритация комплексного числа
Любое комплексное число представляется геометричесмки точкой координатной плоскости XOY ри этом действительная чапсть комплексного числа откладывается по осо OX, а мнимая – по оси Oyежду множествомкомплексных чисел и множнством толчек плоскости XOY сущзествует взаимооднозначное соответствие.
y 



 M
M
b z
 |
x
Если соединить точку, представляющую комплексное число с началом координат, то получим радиус – вектор, который также является геометрическим представлением комплексного числа на плоскости.
Пользуясь геометрическим представлением комплексного числа в векторной форме можно действия сложения и вычитания комплексных чисел производить геометрически, т.е. используя теорему векторов.
§ 1.7 Модуль и аргумент комплексного числа
Модулем комплексного числа называется длина радиус – вектора, который его изображает
│z │= │ │ ==>
│ ==> 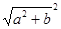
Угол, который образует радиус – вектор, изображающий комплексное число, с осью абсцисс, называется аргументом комплексного числа (Arg z)
Arg z имеет бесконечное множество значений, которые отличаются между собой числом полных оборотов. Среди этого множества выделяется главное значение аргумента, которое имеется в промежутке [-π; π]
Arg z 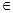 [-π; π]
[-π; π]
 Частные случаи:
Частные случаи:
Arg z = arctg b/a; I, IV четверть =0,a<0, b<0
arctg b/a + π; IIч. = π,a=0, b=0
= - π/2, a=0, b<0
Arctg b/a - π; угол в III ч. =π/2,a=0,b>0
§ 1.8 Тригонометрическая форма комплексного числа
В полярной системе координат положения точкит M определяется ее расстоянием от полюса и углом θ, образованным лучом ОМ с полярной осью. θ считается положительным при отсчете от полярной оси против часовой стрелки.
Если начало декартовой прямоугольной системы координат совместить с полюсом, а ось OX направить по полярной оси, то прямоугольные координаты точки М(x; y) и ее полярные координаты М(ρ; θ) связаеы формулой:
 |
М(x; y) x = ρ cos θ ρ = 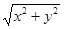
М(ρ; θ) y = ρ sin θ tg θ = y/x









М
x
Z = r(cos φ + i sin φ) - тригонометрическая формула комплексного числа
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 311; Нарушение авторских прав?; Мы поможем в написании вашей работы!