Общие понятия. Дифференциальные уравнения (ДУ)

Дифференциальные уравнения (ДУ).

Профилактика и лечение

Лабораторная диагностика.

Используют методы:

Ø бактериологический – основной;

Ø микроскопический – основной;

Ø серологический.

Материалы для исследования – биоптаты слизистой желудка и двенадцатиперстной кишки. Бактерии распознают по типичным морфологическим особенностям. Для выявления возбудителя в материале обычно применяют фазово-контрастную микроскопию, определяющую характерную подвижность.

Хеликобактеры хорошо видны в гистологических препаратах, окрашенных гематоксилин-эозином или импрегнированных серебром по Уортину-Старри.

Хорошие результаты дает люминесцентная микроскопия мазков, окрашенных акридиновым оранжевым.

В последние годы широко распространены методы косвенного обнаружения H.pylori в биоптатах; чаще всего используют определение уреазной активности (кло-тест); используют такой тест, как обнаружение продуктов распада мочевины в выдыхаемом воздухе.

Для получения чистых культур применяют кровяные среды (5-17% эритроцитов), дополненные антибиотиками (цефсулодин). На 5-7 сутки культивирование при 37⁰С наблюдают видимый рост. Принадлежность культур к хеликобактерам определяют по характерной морфологии микроорганизмов и колоний; «винтообразной» подвижности; способности к росту в микроаэрофильных условиях и отсутствию роста в аэробных и анаэробных условиях и при температуре 25⁰С и 42⁰С.

Из биохимических свойств наиболее часто определяют оксидазную, каталазную и уреазную активности.

Для иммунодиагностики хеликобактериозов используют биоптаты слизистой оболочки желудка и двенадцатиперстной кишки для цитологических и бактериологических исследований и кровь.

В настоящее время разработаны тест-системы для определения Аг хеликобактеров в биоптатах с помощью ИФА, а также в сыворотке в РСК. В крови определяют JgM, JgA, JgG – антитела с помощью ИФА, в ПЦР – гены бактерий.

Для лечения используют полусинтетические пенициллины, аминогликозиды, фторхинолон. Вакцинопрофилактика не разработана.

.

Дифференциальным уравнением называется уравнение, связывающее независимую переменную, некоторую функцию и её производные, т. е. уравнение вида
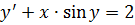является дифференциальным уравнением 1 - го порядка, а уравнение 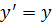и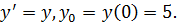

Решение. Общее решение данного уравнения имеет вид 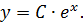Подставим в решение значения переменных 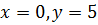, получим равенство
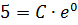, из которого находим 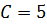. Отсюда решение Задачи Коши для данного уравнения имеет вид .

Уравнения с разделяющимися переменными.

Простейшим ДУ первого порядка является уравнение вида

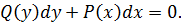
Перенесем слагаемое с 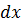в левую часть и возьмем интегралы (проинтегрируем) от обеих частей

=

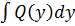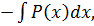
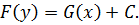
Выразим, если это возможно, из последнего равенства переменную 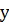и запишем решение уравнения в виде .

В общем случае уравнением с разделяющимися переменными называется уравнение вида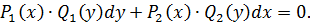

Коэффициенты пр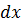и и 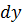представляют собой произведения двух функций, одна из которых зависит только от , другая – только от .

Решение таких уравнений осуществляется следующим образом:

1) переносят все выражения с 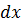вправо, а с 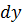– влево

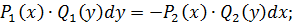
2) делают так, чтобы при 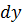функции не содержали переменную , а при 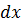– переменную . Обычно это достигается делением обеих частей на выражение на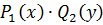

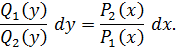В результате получают уравнение с разделенными переменными.

3) Интегрируют его обе части

Отсюда получают общий интеграл 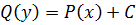, из которого затем выражают (если это возможно) функцию .

Замечание 1. При делении обеих частей уравнения на выражение

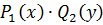могут быть потеряны решения дифференциального уравнения вида 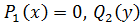=0. Такие решения называются особыми и исследуются отдельно.

Замечание 2. Уравнения вида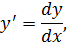

затем домножить обе части на 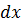, в результате получается уравнение

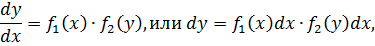
отсюда получают уравнение с разделенными переменными вида

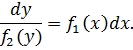
Пример 109. Записать общее решение уравнения

Решение. Данное ДУ является уравнением с разделяющимися переменными поэтому запишем его в виде

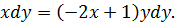
Разделим обе части на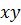

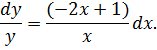
Интегрируем

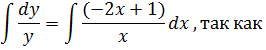
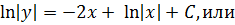
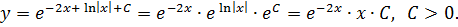
Проверим особые решения: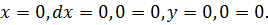

Ответ.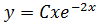. Особые решения , .

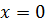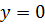Пример 110. Записать общее решение уравнения

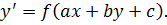
Уравнение вида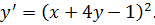

Решение. Сделаем подстановку 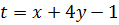. Тогда

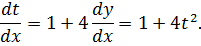
Или
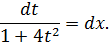Интегрируем

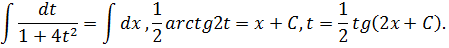
Делаем обратную подстановку и выражаем

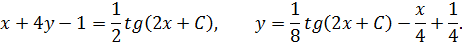
Дата добавления: 2014-01-04