Розрізняють три випадки застосування критерію Найквіста

1. Розімкнута система стійка. В цьому випадку для стійкості замкнутої системи необхідно і достатньо, щоб амплітудно фазова характеристика розімкнутої системи при зміні ω від 0 до ∞ не охоплювала точку з координатами [-1, j0].

Розглянемо можливі ситуації.

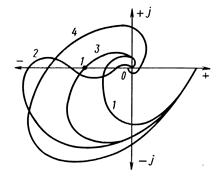1 - замкнута система абсолютно стійка, тобто вона залишається стійкою при зменшенні передаточного коефіцієнта розімкнутої системи.

2 – замкнута система умовно стійка. Вона залишається стійкою тільки при значенні К, яке знаходиться в деяких межах.

3 – крива проходить через критичну точку [-1]. Це означає, що замкнута система знаходиться на коливальній границі стійкості.

4 – крива охоплює критичну точку [-1], замкнута система нестійка.

2. Розімкнута система на границі стійкості. Характеристичний поліном такої системи має нульові чисто уявні корені, а в інших коренях від’ємні дійсні частини.

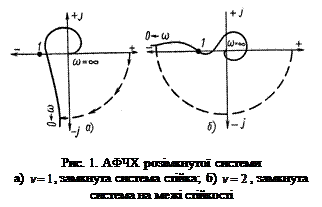Якщо нульових коренів v, то АФЧХ при ω=0 дугою нескінченно великого радіусу переміщується від додатної дійсної піввісі на кут за годинниковою стрілкою. (рис. а, б)

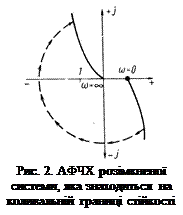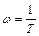Якщо є пара чисто уявних коренів (в знаменнику частотної передаточної функції є множник ), то АФЧХ при частоті дугою нескінченно великого радіусу переміщується на кут 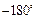(за годинниковою стрілкою рис. 2).

В обох випадках для стійкості замкнутої системи необхідно і достатньо, щоб АФЧХ розімкнутої системи при зміні ω від 0 до ∞, доповнена на ділянці розриву дугою нескінченно великого радіуса, не охоплювала точку з координатами [-1, j0].

Приклад. Дослідити на стійкість розімкнену систему передаточна функція якої

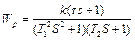
Визначимо частотну передаточну функцію розімкнутої системи. Для цього потрібно чисельник та знаменник помножити на комплексне число спряжене із знаменником і виділити дійсну і уявну частину.

,

,

.

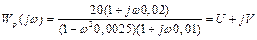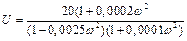Характеристичний поліном має чисто уявні корені 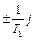(в знаменнику частотної передаточної функції є множник ).

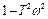Змінюючи ω визначимо значення U і V, результати зведемо в таблицю:

ω
U		21,4	26,9	31,7	46,8	-37,6	-26	-17,3	-10,8	-7,9
V		1,06	2,64	3,7	6,71	-8,36	-6,12	-4,4	-3,02	-2,38

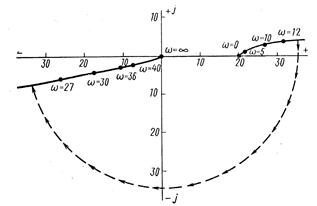При частоті 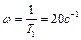АФЧХ має розрив.

Якщо цю криву доповнити дугою нескінченно великого радіуса, то точка з координатами [-1, j0] буде знаходитися поза контуром. Відповідно замкнута система буде стійкою.

3. Розімкнута система нестійка. В цьому випадку критерій Найквіста формулюють так: для стійкої замкнутої системи необхідно і достатньо, щоб при зміні ω віл 0 до ∞ вектор, початок якого знаходиться в точці з координатами [-1, j0], а кінець на АФЧХ розімкненої системи повернувся в додатному напрямку (проти годинникової стрілки) на кут .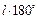

Початок вектора розміщений в точці -1, а кінець описує криву повертаючись проти годинникової стрілки на кут рівний π. Відповідно замкнута САК стійка (рис. 3).

При складній формі АФЧХ розімкненої системи зручно застосовувати інше формулювання критерія Найквіста яке використовує правила переходів.

Перехід АФЧХ при збільшенні ω через відрізок дійсної вісі від -1 до ∞ згори вниз вважають додатнім, а знизу вгору від’ємним.

Критерій формулюється так: замкнута система стійка, якщо між числом додатних і від’ємних переходів АФЧХ розімкненої системи через відрізок дійсної вісі від -1 до -∞ дорівнює .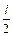

Де – число коренів характеристичного полінома розімкненої системи з додатною частиною.

Дата добавления: 2014-01-04