Робота сили Лоренца

Узагальнена сила Лоренца.

Як відомо, на електричний заряд діє не тільки магнітне, але й електричне поле. Отже, якщо електричний заряд рухається в електромагнітному полі, то сила, яка на нього діє, може бути представлена як векторна сила електричної та магнітної скла­дових:

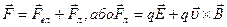
Даний вираз називається узагальненою силою Лоренца.

Нам відомо, що робота сили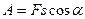

де s — переміщення частинки, здійснене під дією сили F, а 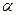- кут між напрямами сили й переміщення. Оскільки сила Лоренца перпен­дикулярна до напряму швидкості руху частинки то cos a =0 і робота сили Лоренца дорівнює нулю.

Відомо, що коли швидкість матеріальної точки пер­пендикулярна до напряму сили, що на неї діє, то ця точка рухається по колу. Значить, електричний заряд у магнітному полі буде рухатися по колу. Слід наголосити, що магнітна сила при цьому є доцентровою. Таким чином, хоча магнітне поле й діє на частинку з деякою силою, але воно змінює тільки напрям руху частинки й не змінює її кінетичної енергії.

16. Рух зарядженої частинки в маг­нітному полі.

Рух зарядженої частинки при 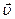перпендикулярна .

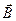Сила Лоренца має максималь­не значення, якщо частинка рухається в площині, перпендикулярній до ліній магнітної індукції (). З курсу механіки відомо, що коли сила Лоренцо перпендикулярна швидкості, то вона надає тілу доцентрового прискорення 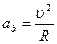і викликає рух тіла по колу радіусом R.

Радіус цього кола можна обчислити, використовуючи другий закон Ньютона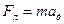

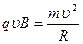, звідки радіус кола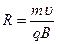

Сила Лоренца роботи не виконує, тому кінетична енергія зарядже­ної частинки, що потрапила в однорідне магнітне поле, не змінюється. Рухаючись по колу зі швидкістю, заряджена частинка зробить один повний оберт протягом часу: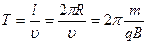

період оберту зарядженої частинки Т по колу не залежить від швидкості, з якою частинка потрапляє в магнітне поле.

Фізичний зміст цієї особливості полягає в тому, що швидші частин­ки рухаються по колу більшого радіуса.

Рух зарядженої частинки при паралельна .

Коли частинка влітає в магніт­не поле зі швидкістю, напрямленою уздовж вектора магнітної індукції В, то кут а = 0. При цьому F_л = 0, тобто магнітне поле не чинить силової дії на частинку, напрям швидкості якої збігається з напрямом вектора В.

Загальний випадок руху зарядженої частинки в однорідному маг­нітному полі.

Одним із складових рухів у даному випадку є рівномірний рух уз­довж поля В зі швидкістю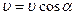, а другим — рух по колу в пло­щині, перпендикулярній до поля. Значення поперечної складової швид­кості дорівнює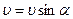

Радіус кола добувається із співвідношення: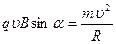

звідки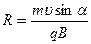

Таким чином, частинка, одночасно беручи участь у двох рухах (рівно­мірному уздовж поля й по колу в поперечній площині), рухається по спіралі. Радіус спіралі вже знайдений. Знайдемо тепер крок спіралі — відстань по осі спіралі, на яку частинка переміщається за один оберт:

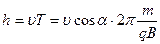
Дата добавления: 2014-01-04