Функція ризику

Моделювання та оптимізація ризику.

Для дослідження статистичних моделей за умов ризику та невизначеності ви­хо­дять із схеми, що передбачає наявність:

- у суб’єкта керування – множини взаємовиключаючих рішень Х = {х₁, х₂, …, х_м}, одне з яких йому необхідно прийняти;

- множини взаємовиключаючих станів економічного середовища, однак, суб’єктові керування невідомо, у якому стані буде знаходитись середовище;

- у суб’єкта керування – функціонал оцінювання F = {f_kj}, що характеризує “виграш” чи “програш” під час вибору рішення х_к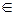Х, якщо середовище знаходиться (буде знаходитися) у стані Ø_j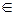Ø.

Творча складова прийняття рішень за умов ризику має вирішальне значення. Формальна складова процесу прийняття рішення за умов невизначеності полягає у проведенні розрахунків, за існуючими алгоритмами, показників ефективності, що входять у визначення функціоналу оцінювання F={f_kj}, та розрахунків для знаходження оптимального розв’язку х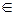^*Х (чи множини таких розв’язків Х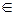^*Х), згідно з обраними критерієм прийняття рішень. Функціонал оцінювання F має позитивний інгредієнт, якщо намагається досягнути 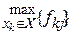(10.25)

Для таких випадків записують F=F⁺={f_kj⁺}.

Для негативного інгредієнта, якщо намагаються досягнути відповідно записують

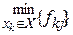, (10.26)

F=F ^-={f ^-_kj}.

Визначення функціоналу оцінювання у формі F=F⁺, як правило, використовується для оптимізації категорії корисності, виграшу, ефективності, ймовірності досягнення цільових подій, тощо. У формі F=F ^- - використовують для оптимізації збитків, ризику, тощо.

Так звана функція ризику визначається як лінійне перетворення позитивно чи негативно заданого інгредієнта функціоналу оцінювання до відносних одиниць вимірювання. Таке перетворення встановлює початок відліку функціоналу оціню­вання для кожного стану економічного середовища Ø_j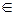Ø:

1) для F⁺,коли мають зафіксований стан середовища Ø_j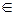Ø знаходять

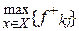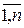l_j = ; j=; k=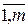; (10.27)

функція ризику визначається у виді

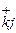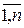r_kj = r_j(x_k) = l_j – f ; j=; k=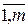; (10.28)

2) для F ^-, при фіксованих Ø_j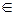Ø знаходять

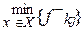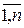L_j = ; j=; k=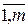; (10.29)

функція ризику визначається у вигляді

r_kj = r_j(x_k) = f 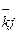- L_j; j=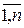; k=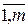; (10.30)

2.2. Критерії прийняття рішень при заданому розподілі ймовірностей. Спочатку дамо визначення інформаційної ситуації.

Під інформаційною ситуацією J розуміють певний ступінь градації невиз­на­че­ності вибору середовищем своїх станів у момент прийняття рішення.

За класифікатором інформаційних ситуацій, пов’язаних з невизначеністю середовища, виділяють шість інформаційних ситуацій:

· J₁ – характеризується заданим розподілом апріорних ймовірностей на еле­мен­тах множини Ø;

· J₂ – характеризується заданим розподілом ймовірностей з невідомими па­ра­метрами;

· J₃ – характеризується заданою системою лінійних співвідношень на компо­нентах апріорного розподілу станів середовища;

· J₄ – характеризується невідомим розподілом ймовірностей на елементах множини Ø;

· J₅ – характеризуються антагоністичними інтересами середовища у процесі прийняття рішень;

· J₆ – характеризуються як проміжні між J₁ та J₅ при виборі середовища своїх станів.

Отже, перша інформаційна ситуація J₁ має місце тоді, коли мають апріорний розподіл ймовірностей

P= (p₁, p₂, …, p_j), p_j = p (Ø=Ø_j), 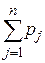=1 на елементах Ø_j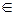Ø.

Ця ситуація є, мабуть, найбільш розповсюдженою в більшості практичних задач прийняття рішень за умов ризику. При цьому ефективно використовуються конструктивні методи теорії ймовірностей та математичної статистики. Розглянемо один із критеріїв прийняття рішень у цій ситуації.

Критерій Байєса

Суть критерію – максимізація математичного сподівання функціоналу оціню­ван­ня. Назва критерію пов’язана з перетворенням формул апріорних ймовір­но­с­тей у апостеріорні. Критерій Байєса часто називають критерієм середніх (сподіва­них) затрат (критерієм ризику при F=F ^-). Згідно з критерієм Байєса оптимальними розв’язками х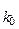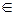Х (або множиною та­ких оптимальних рішень) вважаються такі рішення, для котрих математичне спо­дівання функціоналу оцінювання досягає найбільшого можливого значення.

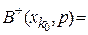
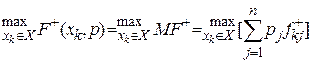. (10.31)

Якщо максимум досягається на декількох рішеннях з х, множину яких позна­чимо через 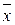, то такі рішення називають еквівалентними. Величина 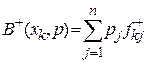називається байєсівським значенням фун­к­ці­о­на­лу оцінювання для рішення 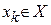. Критерій Байєса є найбільш розповсюдженим в інформаційній ситуації J₁. Цей критерій тісно пов’язаний з аксіомами теорії ко­рисності (аксіома Неймана та Моргенштерна), де сумарна сподівана корисність визначається як математичне сподівання корисностей окремих результатів.

Якщо функціонал оцінювання задано у формі F ^-, то замість оператора max ма­те­матичного сподівання використовується min математичного сподівання. Якщо фу­нкціонал оцінювання задано в ризиках, то сподівану величину B^- (x_k,p) нази­вають байєсівським ризиком для розв’язку x_k .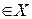

У першій інформаційній ситуації J₁ при прийняті рішень за умов ризику ко­ри­с­туються апріорними ймовірностями.

2.3. Критерії прийняття рішень, коли невідомий розподіл ймовірностей. Інформаційна ситуація J₄ характеризується невідомим розподілом P=(p₁,…, p_n), p_j= P{Ø=Ø_j}, 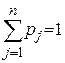на елементах Ø, з одного боку, та відсутністю активної протидії середовища цілям щодо прийняття рішень суб’єктом керування з іншого. Поводження “пасивної природи”, що досліджується у теорії статистичних рішень, та середовища співпадає. Інакше кажучи, ситуація J₄ характеризується цілковитим незнанням суб’єктом керування про те, що стосується ймовірності поводження середовища.

На практиці такі ситуації виникають, коли впроваджуються на підприємствах зразки нової техніки, коли мова йде про реалізацію нових зразків товарів народного споживання, коли зовсім невідомий попит, а також при відпрацюванні у виробництві нових технологічних способів, транспортних маршрутів тощо.

Критерій Бернуллі-Лапласа

В основу цього критерію покладено відомий “принцип недостатніх підстав”. Він вперше був сформульований Бернулі і в загальних рисах означає: якщо немає да­них для того, щоб вважати один стан середовища з множини Ø більш ймо­вір­ним, ніж будь-який інший стан середовища з множини Ø, то апріорні ймовірності p_j станів середовища треба вважати рівними, тобто згідно з принципом недостатніх підстав точкові оцінки визначаються так 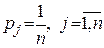. (10.32)

Ці оцінки розподілу апріорних ймовірностей дозволяють застосовувати критерії першої інформаційної ситуації J₁.

Критерій Бернуллі-Лапласа, що ґрунтується на застосуванні критерію Байєса та принципу недостатніх підстав для одержання оцінок апріорних ймовірностей p_j, формулюється таким чином.

Оптимальним згідно з критерієм Бернуллі-Лапласа є те рішення 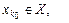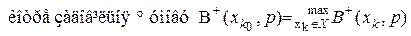де 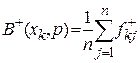(10.32)

Таким чином, можливі стани розглядаються як рівноймовірні, якщо немає жодних відомостей про умови, за яких кожний стан може відбутися.

Домінування розв’язку х_к над розв’язком х_i можна гарантувати у тому і лише в тому випадку, коли 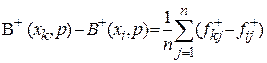(10.33)

Тому необхідною і достатньою умовою пріоритету розв’язку х_к з множини Х є використання нерівності 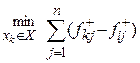0 (10.34)

Принцип максимуму Гіббса-Джейнса

Згідно з принципом Гіббса-Джейнса найбільш характерними розподілами ймо­ві­р­ностей станів невизначеного середовища є такі розподіли, котрі максимізують ви­брану міру невизначеності при заданий інформації щодо поводження середо­вища.

Тут використовується формалізм відтворення невідомих законів розподілу випадкової величини за наявності обмежень з умов максимуму ентропії Шеннона:

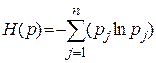(10.35)

Необхідно зазначити, що Н(р) являє собою міру невизначеності, що знаходиться з розподілу апріорних ймовірностей р станів середовища.

Формалізм Джейнса постулює: найменш сумнівним розподілом ймовірностей буде такий, що максимізує невизначеність при врахуванні всієї заданої інформа­ції.

Застосування принципу максимальної невизначеності Гіббса-Джейнса за умов ін­формаційної ситуації J₄ дозволяє визначити точкову оцінку з умов

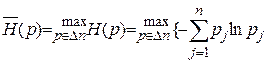(10.36)

у виді 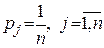. Однак точкова оцінка апріорного розподілу станів середовища постулюється також принципом Бернуллі-Лапаса.

Суттєвою перевагою принципу максимальної невизначеності Гіббса-Джейнса є те, що існує можливість одержання оцінок апріорного розподілу, в яких суб’єктом керування можуть бути накладені обмеження на розподіл апріорних ймовірностей станів середовища, наприклад, у формі задання середніх та дисперсій (ризику) характеристик значень функціоналу оцінювання F.

Дата добавления: 2014-01-04