Підприємств

Оптимізація оподаткування

Розглянемо економічну ситуацію щодо дій уряду держави з оподаткування підприємств в фірм і визначимо, як пов’язані прибуток фірми та обсяг податків, що надходять державі за даної податкової ставки. Нехай ціна на продукцію p (q) = a – b q, a > 0, b > 0, тобто лінійно зменшується зі збільшенням обсягу готової продукції на ринку, а витрати C = C (q) залежать від обсягу продукції q таким чином: C (q) = c q² + d q + e, де a, b, c, d, e - деякі додатні числа. Нехай податок є акцизом зі ставкою t, тобто з кожної проданої одиниці товару держава одержує податок t, і податкова сума становить T = t q. Тоді фірма має прибуток

P (q) = p q – C (q) – T = q (a – b q) – c q² – d q – e – t q.

Для того щоб максимізувати прибуток, фірма шукає оптимальний обсяг виробництва. Обчислимо похідну функції прибутку:

P’(q) = a – 2 b q – 2 c q – d – t = a – d – t – 2 q (b + c)

Перевіримо необхідні умови екстремуму. Для цього прирівняємо до нуля похідну функції прибутку: P’ (q) = 0, 2 q (b + c) = a – d – t. Дістанемо критичну точку:

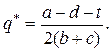
Оскільки P’’ (q) = - 2 (b + c) < 0, то згідно з достатніми умовами локального екстремуму q^* – справді точка максимуму.

Оскільки t > 0, то така податкова ставка призводить до зниження оптимального випуску продукції.

Для прогнозування дій уряду зі встановлення податкової ставки t обчислимо податковий доход держави:

,

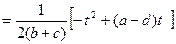Тобто в даній країні крива доходів держави є параболою, вітки якої напрямлені вниз.

Знайшовши похідну 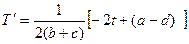, визначимо критичні точки з умови T’ = 0, тобто 2 t = a – d,

Оскільки друга похідна 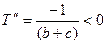, то максимум досягається при і становить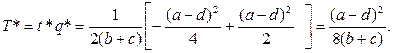

Оптимальний випуск продукції при цьому значенні t^* становить 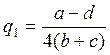, і відповідний прибуток фірми .

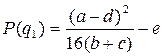Взагалі прибуток фірми за податкової ставки t ,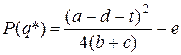

звідки випливає, що зі збільшенням податкової ставки t прибуток фірми зменшується, якщо 0 ≤ t ≤ a – d, і існує область значень податкової ставки при 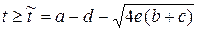, в якій прибуток фірми від’ємний, хоча доходи держави додатні. Це відбувається тому, що за критерій вибору обсягу випуску було взято максимум прибутку фірми, але не було обумовлено, що цей максимум має бути додатним.

Якщо вважати, що при 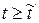випуск продукції справді стане нульовим, то доход держави при 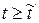також дорівнюватиме нулю. Тому зрозуміло, що вже біля 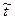відбувається різке скорочення ділової активності.

Приклад. Нехай t - податкова ставка. Відомі функція доходу R (q) = 16 q – q² і функція витрат C (q) = q² + 1 фірми. Визначимо, яким має бути податок t, щоб сумарний податок T з усієї продукції був найбільшим.

Запишемо функцію прибутку фірми P (q) = R (q) – C (q) – T. У нашому випадкові

P (q) = 16 q – q ² – q² – 1– t q= 16 q – 2 q² – t q – 1.

З’ясуємо, при якому значенні функція прибутку набуває максимального значення. Оскільки необхідна умова максимуму прибутку P’ (q) = 0, то P’ (q) = 16 – 4 q – t. Розв’яжемо рівняння 16 – 4 q – t =0, або 4 q =16– t. Отже, q ^* = 4 – t / 4. Оскільки P’’ (q) = – 4 < 0, то q^* – точка максимуму. Отже, оптимальний обсяг q^*= q_опт.

Підставимо добуте значення обсягу продукції у вираз сумарного доходу:

І знайдемо умови, за яких T буде максимальним.

Обчислимо похідну: Знаходимо стаціонарні точки: T’ = 0. Дістанемо 4 – t / 2 = 0, t = 8. Тоді q^* = 4 – 8 / 4 = 4 – 2 = 2.

Обчислимо максимальний прибуток фірми:

P_max = P (q) = 16 ∙2 – 2 ∙ 2² – 8 ∙2 – 1 = 32 – 8 – 16 – 1 = 7

Оптимальний з погляду податкового законодавства акцизний податок

T = 2 ∙ 8 = 16.

Цікаво порівняти ці цифри з цифрами в разі відсутності оподаткування. При t = 0 розв’язок задачі на знаходження максимуму функції прибутку дав би такі результати: q = 4, P_max = 31.

Отже, зменшення оподаткування стимулює збільшення випуску продукції й сприяє збільшенню прибутку від її реалізації. Зрозуміло, чому виробники докладають стільки зусиль, щоб знизити податкову ставку.

Дата добавления: 2014-01-04