Необходимый признак сходимости

Теорема 47. Если ряд
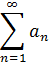сходится, то

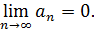
Доказательство. Пусть исходный ряд сходится и
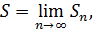тогда и
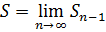Так как 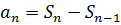, то

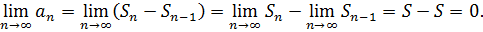
Следствие 1. (Достаточное условие расходимости ряда). Ели предел общего члена ряда не равен нулю
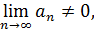то ряд расходится.

Действительно, если бы ряд сходился, то выполнялось бы условие теоремы, что противоречит допущению следствия.

Пример 126. Проверить необходимое условие сходимости следующего числового ряда

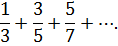
Решение. Числители и знаменатели членов ряда образуют арифметические прогрессии с разностью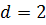, поэтому

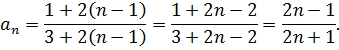
Отсюда

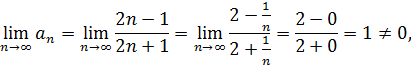
Необходимое условие сходимости ряда не выполняется и по следствию 1 исходный ряд расходится.

Пример гармонического ряда показывает, что из выполнения необходимого признака сходимости не всегда следует сходимость числового ряда. То есть этого признака недостаточно для исследования сходимости числовых рядов. Поэтому сходимость рядов во многих случаях определяется с помощью других (достаточных) признаков.

Дата добавления: 2014-01-04