Метод найбільшої правдоподібності

Слід зауважити, що метод моментів є найпростішим методом оцінювання параметрів розподілу за вибірковими даними. Окрім методу моментів існують і інші методи оцінювання точкових характеристик невідомих параметрів розподілу. До них належить, наприклад, метод найбільшоїправдоподібності. Суть цього методу полягає в наступному.

Нехай розподіл випадкової величини 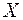у генеральній сукупності має щільність ймовірностей 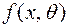, яка визначається одним невідомим параметром 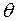. Необхідно визначити точкову оцінку цього параметру. Оскільки всі варіанти вибіркової сукупності розглядаються як незалежні випадкові величини, то щільність ймовірностей для вибірки дорівнює добутку щільності ймовірностей щодо кожної з варіант. Отже, отримуємо функцію щільності ймовірностей у вигляді:

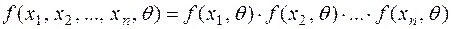. (11.5)

Функція 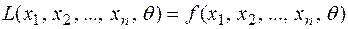, де 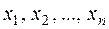– фіксовані числа, називають функцієюправдоподібності. Вона залежить від параметру .

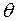Для дискретної випадкової величини функцію правдоподібності записують відносно ймовірності. У цьому випадку вона має вигляд:

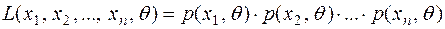. (11.6)

Статистична точкова оцінка 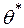називається оцінкою найбільшої правдоподібності, якщо при 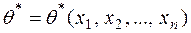функція правдоподібності сягає максимуму.

За звичай розглядають не саму функцію правдоподібності, а її натуральний логарифм 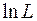. Для визначення точки максимуму цієї функції необхідно спочатку знайти стаціонарну точку за умови, що 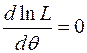(необхідна умова екстремуму), а потім перевірити, чи виконується для стаціонарної точки достатня умова екстремуму: 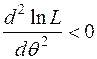. Якщо ця умова виконується, то ми знайшли точкову оцінку .

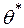Метод найбільшої правдоподібності має ряд переваг перед методом моментів. Так, метод найбільшої правдоподібності забезпечує найменшу є можливих дисперсію оцінок, тобто за цим методом ми отримуємо ґрунтовні оцінки.

Якщо для параметра, що досліджується, існує ефективна оцінка, то за методом найбільшої правдоподібності ми отримуємо єдиний розв’язок для статистичної оцінки 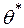. Цей метод найбільш повно використовує дані вибіркової сукупності, тому від особливо корисний при дослідженні малих вибірок. Однак його суттєвий недолік полягає у тому, що він потребує складних обчислень.

Приклад. За теоретичними міркуваннями розподіл неперервної випадкової величини можна вважати експоненціальним. За методом найбільшої правдоподібності визначити точкову оцінку параметру розподілу.

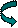Розв’язання. Відомо, що показниковий закон розподілу неперервної випадкової величини описується функцією щільності ймовірностей, яка має вигляд:

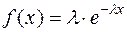, де .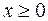

Згідно з формулою (11.5) функція правдоподібності в цьому випадку набуває вигляду:

.

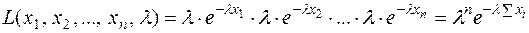Запишемо необхідну умову екстремуму 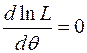і звідси маємо:

.

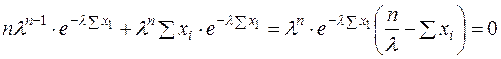Отже, після перетворення для визначення статистичної оцінки отримуємо рівняння:

.

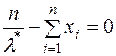
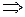
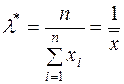Перевіряємо достатню умову екстремуму. Для цього визначаємо знак другої похідної від функції правдоподібності у стаціонарній точці. Так, 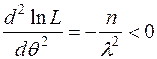, отже у точці 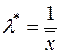маємо максимум функції правдоподібності. Це той самий розв’язок, що і за методом моментів.

Ще одним поширеним методом, який застосовується для оцінювання параметрів теоретичного розподілу, є метод найменших квадратів, але його доцільно застосовувати для визначення параметрів розподілу багатовимірних випадкових величин, тому розглянемо його тоді, коли розглядатимемо питання кореляційного та регресійного аналізів.

Дата добавления: 2014-01-04