Ознаки мультиколінеарності

Мультиколінеарність.

1. Основні теоретичні положення

На практиці при кількісному оцінюванні параметрів економе-тричної моделі часто стикаються з проблемою взаємозв'язку між пояснюючими змінними. Якщо такий взаємозв'язок досить тісний, то оцінки параметрів моделі можуть мати зміщення. Такий взаємозв'язок між пояснюючими змінними називається мультиколінеарністю. Мультиколінеарність пояснюючих змінних при­зводить до зміщення оцінок параметрів моделі, обчислюваних за методом 1 МНК. На підставі цих оцінок не можна дійти конкретних висновків про результати взаємозв'язку між пояснюваною і пояснюючими змінними.

1. Якщо серед парних коефіцієнтів кореляції пояснюючих змін­них є такі, рівень яких наближається до множинного коефіцієнта кореляції або дорівнює йому, це свідчить про можливість існуван­ня мультиколінеарності. Інформацію про парну залежність може Дати симетрична матриця коефіцієнтів парної кореляції, або, як її Ще називають, матриця кореляції нульового порядку:

Проте якщо в моделі включено більш як дві пояснюючі змінні, вивчення питання про мультиколінеарність не може обмежува­тись інформацією, яку дає ця матриця. Явище мультиколінеарності в жодному разі не зводиться лише до існування парної коре­ляції між пояснюючими змінними.

Загальніша перевірка передбачає застосування визначника (детермінанта) матриці г, який називається детермінантом коре­ляції і позначається | г|. Числові значення детермінанта кореляції містяться на інтервалі |г| є [0,і].

2. Якщо |г| = 0, то існує повна мультиколінеарність. У разі |г| = 1 мультиколінеарність відсутня. Чим ближче \г\ до нуля, тим певніше можна стверджувати, що між пояснюючими змін­ними існує мультиколінеарність. Незважаючи на те, що числове значення |г| зазнає впливу дисперсії пояснюючих змінних, цей показник можна вважати точковою мірою рівня мультиколіне-арності.

3. Якщо в економетричній моделі знайдено мале значення па­раметра а_к в разі високого рівня коефіцієнта детермінації, це та­кож свідчить про наявність мультиколінеарності.

4. Коли коефіцієнт детермінації і?², який обчислено для регре-сійних залежностей між однією пояснюючою змінною та іншими такими змінними, близький до одиниці, то можна говорити про наявність мультиколінеарності.

5. Якщо при побудові економетричної моделі на основі покро-кової регресії включення нової пояснюючої змінної істотно змі­нює оцінку параметрів моделі при незначному підвищенні (або зниженні) коефіцієнтів кореляції чи детермінації, то ця змінна перебуває, очевидно, у лінійній залежності від інших, які було введено в модель раніше.

Усі ці методи виявлення мультиколінеарності мають один спі­льний недолік: жодний із них чітко не розмежовує випадок, коли мультиколінеарність, яку слід вважати «істотною» та неодмінно враховувати, і випадок, коли мультиколінеарністю можна знех­тувати.

Алгоритм Фаррара — Глобера

Найповніше дослідити мультиколінеарність можна за допомо­гою алгоритму Фаррара—Глобера. Цей алгоритм містить три види статистичних критеріїв, згідно з якими перевіряється відповід­но мультиколінеарність: а) усього масиву пояснюючих змінних (Х², — <да-квадрат»); б) кожної пояснюючої змінної з рештою

пояснюючих змінних (F-критерій); в) кожної пари пояснюючих змінних (/-критерій).

Усі ці критерії при порівнянні з їх критичними значеннями дають змогу зробити конкретні висновки щодо наявності чи від­сутності мультнколінеарності пояснюючих змінних.

Опишемо алгоритм Фаррара—Глобера.

Крок 1. Нормалізація змінних.

Нехай Х\, Хі, Аз,..., Х_т — вектори пояснювальних змінних економетричної моделі. Елементи стандартизованих векторів об­числимо за формулою:

де п — число спостережень \і = \,п); in — число пояснювальних чмінних [к = \, /;/); Хк — середня арифметична к-'і пояснюваль­ної змінної; a²_Vt —дисперсія к-'і пояснювальної змінної.

Крок 2. Знаходження кореляційної матриці першого по­рядку

де Х* — матриця нормалізованих пояснювальних змінних;

X*’ —матриця, транспонована до матриці X*.

Крок 3. Визначення критерію <ш'-квадрат»:

Де | r | — визначник кореляційної матриці r.

Значення цього критерію порівнюється з табличним за таких

умов: 1/2т(т-1) ступенів свободи і рівень значущості а. Якщо

Цих, < Хтабл > ^{т0 в} масиві незалежних змінних мультиколінеар-"ість відсутня. ^д

Крок 4. Визначення матриці, оберненої до r:

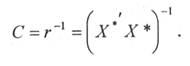
Крок 5. Розрахунок F -критеріїв:

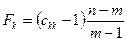
де C_kk — діагональні елементи матриці С. Фактичні значення кри­теріїв Fu порівнюються з табличними, коли маємо т - 1 і п - т ступенів свободи і рівень значущості а. Якщо F_k^_aKT > F_Ta6n, від­повідна А>та пояснююча змінна мультиколінеарна з іншими.

Коефіцієнт детермінації для кожної змінної обчислюється так:

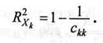
Крок 6. Знаходження частинних коефіцієнтів кореляції:

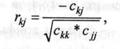
де Ckj — елемент матриці С, що міститься в k-му рядку ij-ьлу стовпці (к = \,т, j - l,m, Скк і сц — діагональні елементи матриці Q.

Крок 7. Розрахунок f-критеріїв:

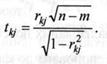
Фактичні значення критеріїв Іщ порівнюються з табличними, коли маємо п-т ступенів свободи і рівень значущості а. Якщо hj факт ^> 'табл ' ^м'^ж ПОЯСНЮЮЧИМИ ЗМІННИМИ Хк І Xj ІСНуЄ МуЛЬТИКО-лінеарність.

1. Дослідження наявності мультикотнеарності згідно з алгоритмом Фаррара — Глобера

Розглянемо застосування алгоритму Фаррара—Глобера для розв'язування конкретної задачі.

Приклад. Оскільки між пояснюючими змінними можлива тіс­на залежність (мультиколінеарність), метод 1 МНК може дати зміщені кількісні характеристики взаємозв'язку. Тому дослідимо наявність мультиколінеарності між пояснюючими змінними, ско­риставшись алгоритмом Фаррара—Глобера.

Якщо виявлено мультиколінеарність, потрібно перетворити певним чином вихідну інформацію, щоб уникнути мультиколіне­арності, а далі знову оцінити параметри моделі методом 1 МНК.

Для дослідження мультиколінеарності наведемо статистичну сукупність спостережень (табл. 1).

Таблиця 1

Необхідно:

1. Обчислити середнє значення та стандартні відхилення.

2. Нормалізувати пояснюючі змінні.

3. Знайти кореляційну матрицю г.

4. Визначити визначник матриці r (det r).

5. Обчислити критерій х²

6. Визначити F-критерії.

7. Визначити частинні коефіцієнти кореляції r.

8. Визначити t-критерії.

9. Зробити висновки щодо мультиколінеарності.

Розв'язання

Для розв'язання використаємо стандартні функції Excel.

1. Обчислимо середні значення та стандартні відхилення по­яснюючих змінних Х\, Xj, Хт,.

Для цього в мастер функції знайдемо категорію «статистичні» і функції «СРЗНАЧ» та «СТАНДВІДХИЛ».

2. Нормалізуємо пояснюючі змінні. _и Серед статистичних функцій знайдемо функцію «НОРМАЛІ­ЗАЦІЯ» та нормалізуємо Х\, Хг, Ху.

Транспонуємо матрицюй (нормалізовану) в матрицю X*'

Перемножимо матриці X*' та^*:

3. Знайдемо кореляційну матрицю г.

Для знаходження кореляційної матриці г необхідно кожний елемент матриці X *' X * помножити на (у нашому випадку и-1 «-1 = 19, оскільки п = 20):

4. Знайдемо визначник матриці r (det r).

Для знаходження det r необхідно серед математичних функцій 6 Excel знайти функцію «МОПРЕД». Скориставшись нею, діста­немо:

Оскільки det r наближається до 0, то в масиві пояснюючих змінних може існувати мультиколінеарність

Прологарифмуємо визначник матриці r.

5. Обчислимо критерій %² за формулою:

Маємо:

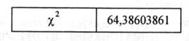
Знайдене значення х² порівнюємо з табличним значенням [ікр² =7,80], коли маємо — т(т-\) = 3 ступенів свободи та при рівні значущості а = 0,05.

ОСКІЛЬКИ Хфакт >Хкрит> ^{то в} МАСИВІ ПОЯСНЮЮЧИХ ЗМІННИХ (прО дуктивність праці, питомі інвестиції та фондовіддача) існує мультиколінеарність.

6. Обчислимо F-критерії.

Безпосередньо F-критерії обчислюються за формулою:

де Скк — діагональний елемент матриці С.

Для визначення F-критеріїв необхідно знайти матрицю С, яка є оберненою до матриці г.

Обчислені F-критерії порівнюються з табличним значенням (F= 5,29), коли єп-т (16) ступенів свободи та при рівні значу­щості а = 0,05.

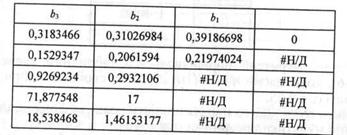
У розглядуваному випадку F\ > F^, F₂ > F^m, F3 > F_Kpm- Це означає, що кожна з пояснюючих змінних мультиколінеарна з іншими.

7 Визначимо частинні коефіцієнти кореляції г. - " Д * Частинні коефіцієнти кореляції показують тісноту зв язку між двома пояснюючими змінними за умови що інші зм.нн. не впли­вають на цей зв'язок і обчислюються за формулою:

Отже, спираючись на здобуті нами значення окремих (частин­них) коефіцієнтів кореляції, можна сказати, що зв'язок між фон­довіддачею та продуктивністю праці є тісним, якщо не врахову­вати вплив питомих інвестицій; зв'язок між фондовіддачею та питомими інвестиціями є слабким, якщо не брати до уваги вплив продуктивності праці. Зв'язок між продуктивністю праці та пи­томими інвестиціями також є слабким, якщо не враховувати фондовіддачу.

8. Визначимо f-критерії.

Ці критерії застосовуються для визначення мультиколінеарно-сті двох пояснюючих змінних і обчислюються за формулою:

Обчислені /-критерії порівнюються з табличним значенням it = 1J46), коли маємо п - т (16) ступенів свободи та при рівні значущості а - 0,05..,

Оскільки t_n > 'крит, то продуктивність пращ та фондовіддача є відповідно мультиколінеарними між собою;

'із > /крит, тому відповідно продуктивність пращ та питомі ін­вестиції є мультиколінеарними між собою;

hi < t_KpHT, тому продуктивність праці та питомі інвестиції не є мультиколінеарними між собою.

Дослідження показали, що мультиколінеарність існує. Отже, для того, щоб можна було застосувати метод 1 МНК для оціню­вання параметрів моделі за цією інформацією, необхідно звільни­тися від мультиколінеарності.

Покажемо, як побудувати економетричну модель методом, 1 МНК на основі нормалізованих даних.

Застосуємо функцію «лінійн» для знаходження всіх оцінок параметрів нової моделі, стандартні похибки цих оцінок, коефіці­єнт детермінації, дисперсію залишків і т. ін.

Щоб обчислити оцінки параметрів моделі в абсолютному ви­разі, скористаємося формулами:

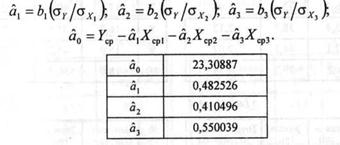
Отже, економетрична модель має вигляд:

де У — дохід; Х\ — фондовіддача; Х₂ — продуктивність праці; -*з — питомі інвестиції.

Дата добавления: 2014-01-04