Чисельні методи розв’язування задачі Коші для систем звичайних диференціальних рівнянь першого порядку

ЛЕКЦІЯ 6

Всі розглянуті чисельні методи розв’язування задачі Коші для звичайних диференціальних рівнянь першого порядку легко переносяться на випадок систем таких рівнянь.

Розглянемо задачу Коші для системи звичайних диференціальних рівнянь першого порядку

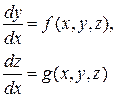(1)

з початковими умовами

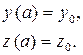(2)

Якщо на проміжку функції та задовольняють теорему Пікара, то задача (1)-(2) має єдиний розв’язок.

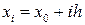
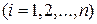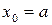Нехай на проміжку задана система розрахункових вузлів , де , – крок.

Аналогічно випадку одного диференціального рівняння, можна вивести формули методу Ейлера для розв’язування задачі Коші (1)-(2):

(3)

,

де , .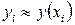

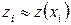Метод Рунге-Куттачетвертого порядку для задачі (1)-(2) виражається формулами:

(4)

де

, , , .

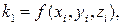
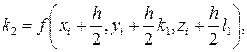
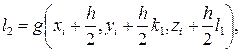
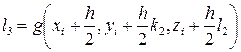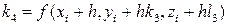(5)

Аналогічно можна узагальнити ці та інші однокрокові й багатокрокові методи на випадок розв’язування задачі Коші для систем звичайних диференціальних рівнянь першого порядку з рівняннями.

Дата добавления: 2014-01-04