Опасное сечение — это поперечное сечение, в котором действуют наибольшие внутренние усилия

А где будет располагаться опасное сечение в более сложном случае нагружения (рис. 1.11, б)? Сразу дать правильный ответ до­статочно трудно, так как сосредоточенный изгибающий момент и распределенная нагрузка 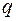изгибают балку вниз, а сосредото­ченная сила 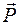— вверх, при этом величины моментов от каждого вида нагрузки различны.

а) б)

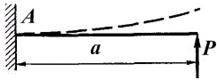
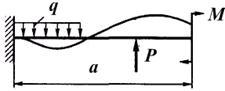
Рис. 1.11

Поэтому для сложных случаев нагружения необходимо знать закон изменения по длине балки изгибающего момента или другого внутреннего усилия (например, продольной силы 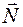, поперечной силы 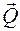или крутящего момента 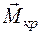). Этот закон можно изобразить с помощью специальных графиков, называемых эпюрами.

Эпюра — это график, изображающий закон изменения внутрен­него усилия по длине стержня.

В случаях растяжения — сжатия (рис. 1.12, а) или кручения (рис. 1.12, б) ординаты эпюр продольных сил или крутящих моментов также показывают их величины в соответствующих поперечных сечениях.

Любое внутреннее усилие определяется по внешним нагрузкам при помощи метода сечений. Каждая эпюра на разных участках имеет различные знаки.

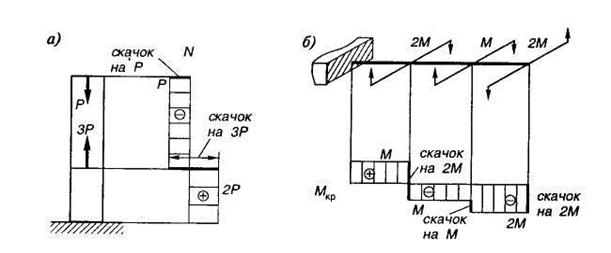
Рис. 1.12

Правила знаков внутренних силовых факторов (ВСФ).

Рассмот­рим правила знаков для внутренних усилий, применяемые в маши­ностроении:

1. Продольная сила 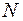считается положительной, если она вызывает растяжение отсеченной части и отрицательной, если вызывает ее сжатие.

2. Поперечная сила 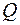считается положительной, если она вращает отсеченную часть по ходу часовой стрелки и отрицательной, если вращение происходит против хода часовой стрелки.

3. Изгибающий момент положителен, если сжаты верхние волокна отсеченной части, и отрицателен, если сжаты нижние волокна. Эпюра изгибающих моментов строится на сжатых волокнах.

4. Правило знаков для крутящего момента удобно принимать произвольным.

Запишем выражение изгибающих моментов для текущегосечения z, например, в консольной балке, находящейся под действи­емсосредоточенной силы (рис. 1.12):

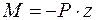— уравнение прямой.

Из этого следует, что на прямолинейном ненагруженном вне­шней пролетной нагрузкой участке стержня эпюра моментов пря­молинейна, а эпюра поперечных сил 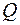постоянна (рис. 1.13, а, б, в).

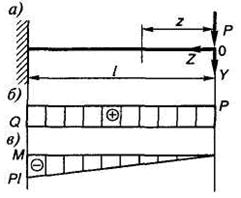
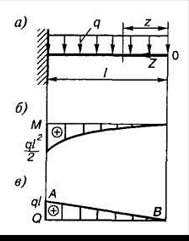
Рис. 1.13 Рис. 1.14

Запишем выражение изгибающих моментов для текущего сечения z в случае изгиба консольной балки, находящейся под действием равномерно распределенной нагрузки (рис. 1.14, а):

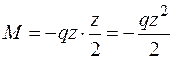
— это уравнение квадратной параболы.

В соответствии с дифференциальной зависимостью Журавского:

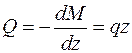— уравнение прямой.

Таким образом, на участке с распределенной нагрузкой эпюры изгибающих моментов очерчены по квадратичной параболе с выпуклостью навстречу действию распределенной нагрузки, а эпюра поперечных сил 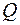имеет вид трапеции или треугольника и ограни­чена прямой наклонной линией АВ, при этом направление наклона (при обходе слева направо) совпадает с направлением 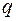(рис. 1.13 и 1.14).

Примеры построения эпюр (рис. 1.15).

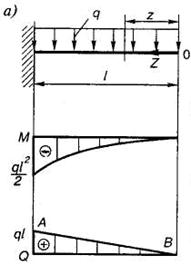
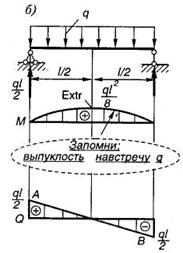
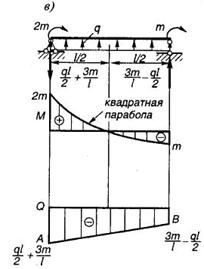
Рис. 1.15

3. напряжения и деформации

Интенсивность, равная величине внутренних сил, приходящихся на единицу площади называется напряжением в точке (рис. 1.16) и является ключевым понятием в сопромате.

Существует 2 вида напряжений:

,

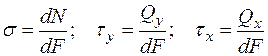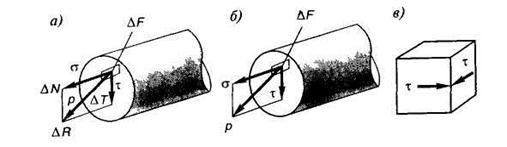
Рис. 1.16

причем 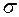(сигма) — нормальное напряжение, действует по нормали (перпендикуляру) к площадке;

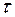(тау) — касательные напряжения, они скользят по площадке, касаются ее (рис. 1.16, в).

Напряжения измеряются в Н / м ² (Па) и МПа. Иногда используют полное напряжение (рис. 1.16, а, б).

.

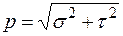Понятие о деформациях. Реальные тела под воздействием внеш­них сил могут изменять свою форму и размеры — деформироваться. Определение величины этих изме­нений называется расчетом на

жест­кость.

Все возможные изменения формы мо­жно оценить, используя всего лишь два вида деформаций — линейные (рис. 1.17) и угловые (рис. 1.18).

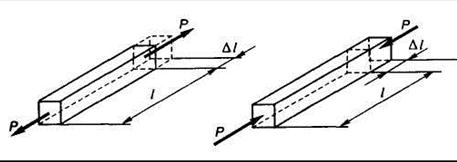
Рис. 1.17

При нагружении растягивающими си­лами стержень удлиняется. Изменение 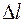первоначальной длины стержня называется абсолютным удлинени­ем.

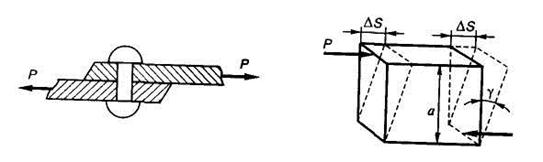
Рис. 1.18

Центральное растяжение (сжатие) возникает в случае, ког­да стержень нагружен силами, совпадающими по направлению с его осью (рис. 1.120). В этом случае из шести внутренних силовых факторов пять равны нулю и только продольная сила .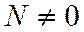

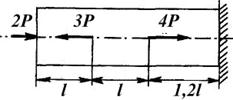
Рис. 1.20

На растяжение, сжатие ра­ботают многие элементы кон­струкций: стержни ферм, ко­лонны, штоки паровых машин и поршневых насосов, стяжные винты, канаты лебедок и другие детали.

Сдвиг или срез возникает, когда внешние силы смещают два параллельных сечения одно относительно другого, при неизменном расстоянии между ними. На сдвиг или срез работают, например, заклепки или болты, скрепляющие элементы, которые внешние силы пытаются сдвинуть (рис. 1.21).

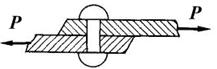
Рис. 1.21 Рис. 1.22

Кручение возникает при действии на стержень внешних сил, образующих моменты от­носительно продольной оси стержня. При этом из шести внутренних сил только 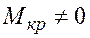. На круче­ние работают валы, шпин­дели токарных и сверлиль­ных станков, роторы дви­гателей и другие детали (рис. 1.22).

Изгиб — это такой вид нагру­жения, когда внешние силы вызыва­ют моменты относительно оси сим­метрии (или главной оси), расположенный в плоскости поперечного се­чения. Этот момент называется изгибающим. Самый простой случай — это плоский изгиб, когда все внешние силы лежат в одной плоскости, совпадающей во всех рассматриваемых нами случаях с плоскостью симметрии (или глав­ной плоскостью) балки.

Дата добавления: 2014-01-04