Умови вертикальної стійкості атмосфери для сухого або ненасиченого повітря

Вертикальна стійкість атмосфери визначається її термічною стратифікацією, тобто залежить від вертикального розподілення в ній температури. Виділимо уявно деяку масу сухого або ненасиченого повітря, що адіабатично піднімається, та будемо зрівнювати її температуру з температурою оточуючого повітря.

Нехай у поверхні землі маса повітря, що підіймалася (рис. 9.2) мала температуру, рівну температурі оточуючого повітря, .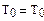

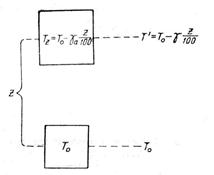
Рис. 9.2. До виведення умов вертикальної стійкості атмосфери.

Тоді на будь-якій висоті z температура маси повітря, що підіймається, буде 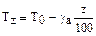, а температура оточуючого повітря 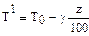, тоді їх різниця:

(9.10)

Припустимо, що в атмосфері температура падає менше ніж на 1º на 100 м, тобто вертикальний температурний градієнт менше сухоадіабатичного: γ < γ_а. При піднятті на 100 м маса повітря, що підіймається, охолоне на 1°, а в оточуючому ж повітрі температура зменшуватиметься з висотою повільніше. Тоді на будь-якій висоті маса повітря, що підіймається, виявиться холодніше (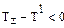), а отже, і щільніше, ніж оточуюче повітря. Надана самій собі, ця маса почне опускатися, щоб повернутися в початкове положення. Тоді стан атмосфери буде стійким.

Припустимо, що в атмосфері температура знижується також на 1° на кожні 100 м висоти, тобто 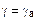. В цьому випадку маса повітря, що підіймається, на будь-якій висоті буде мати температуру, що дорівнює температурі оточуючого повітря (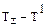= 0), і, надана самій собі, на будь-якій висоті вона залишиться в цьому новому положенні. Такий стан атмосфери називається байдужим.

Нарешті, якщо температура в атмосфері зменшується більше ніж на 1° на 100 м (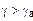), то маса повітря, що підіймається, при охолодженні на 1º на кожні 100 м підняття, на деякій висоті виявиться тепліше оточуючого повітря. Надана самій собі, ця маса повітря продовжить рух угору. Стан атмосфери буде нестійким.

Таким чином, величина вертикального геометричного градієнта температури характеризує вертикальну стійкість атмосфери: якщо

γ < γ - стан атмосфери стійкий,

γ = γ - байдужий,

γ > γ - нестійкий.

Про ступінь стійкості атмосфери можна судити за графіком термічної стратифікації (рис. 9.3). На ньому нанесені прямі, що характеризують фактичне розподілення температури за висотою в атмосфері. Ці прямі будуть мати різний нахил у залежності від значення γ, як це видно із рисунка.

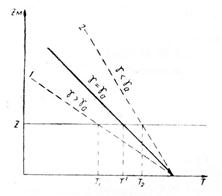
Рис. 9.3. Умови стійкості сухого повітря.

Дійсно, при γ > 1°/100 м на висоті z температура оточуючого повітря 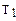менше, ніж температура маси Т´, що адіабатично підіймається, та лінія нестійкої стратифікації 1 проходить ліворуч від сухої адіабати (жирної лінії).

При γ < 1º/100 м на тій же висоті z температура оточуючого повітря більше, ніж маси, що підіймається, а лінія стійкої стратифікації 2 проходить праворуч від сухої адіабати. Очевидно, що при γ = 1°/100 м лінія байдужої стратифікації співпадає з сухою адіабатою.

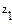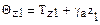Ті ж умови стійкості сухого повітря можна виразити через потенційну температуру. Для цього запишемо значення потенційної температури на висотах і :

і 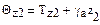(9.11)

Висоти 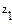і виражені в сотнях метрів, причому 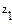< . Зміна потенційної температури з висотою буде

(9.12)

або, якщо розділити обидві частини рівняння на ,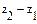

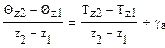, (9.13)

де- зміна потенційної температури з висотою, а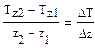 - зміна температури з висотою, тобто вертикальний температурний градієнт.

Оскільки величина градієнта вважається від’ємною при зменшенні температури з висотою, то . Отже, вираз (9.13) прийме вигляд

(9.14)

Звідси робимо наступні висновки:

1) при стійкому стані, коли , величина зміни потенційної температури з висотою додатна; потенційна температура збільшується з висотою;

2) при байдужому стані, коли 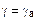, величина ; отже, потенційна температура з висотою не змінюється;

3) при нестійкому стані, коли 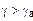, величина 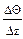буде від’ємна; отже, потенційна температура з висотою зменшується.

Дата добавления: 2014-01-04