Непараметричний тест Гольдфельда-Квандта

Гольдфельд і Квандт для оцінювання наявності гетероскедастичності запропонували також непараметричний тест. Цей тест базується на кількості піків у величини залишків після впорядкування спостережень за x_j.

Закономірність зміни залишків, коли дисперсія є однорідною – явище гомоскедастичності – подано на рис. 8.1., а на рис. 8.2. спостерігається явище гетероскедастичності.

Цей тест, звичайно, не такий надійний, але він досить простий у використанні.

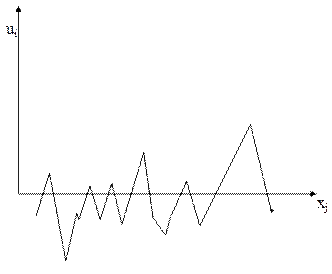
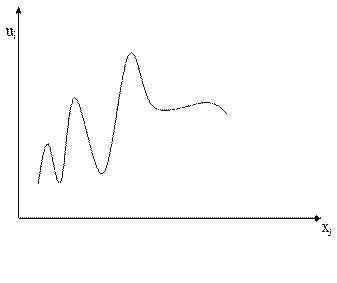
Рис. 8.1. Залишки, що мають постійну Рис. 8.2. Залишки, дисперсія яких

дисперсію змінюється для різних груп спостережень

8.3. Узагальнений метод найменших квадратів (Метод Ейткена)

Економетрична модель, якій притаманна гетероскедастичність, є узагальненою моделлю, і для оцінювання її параметрів слід скористатися узагальненим методом найменших квадратів.

Припустимо, що задано економетричну модель

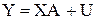(8.8)

коли .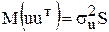

Задача полягає в знаходженні оцінок елементів вектора А в моделі. Для цього використовується матриці S, за допомогою якої коригується вихідна інформація. Ця ідея була покладена в основу методу Ейткена.

Визначимо матрицю S. Оскільки явище гетероскедастичності пов’язане лише з тим, що змінюються дисперсії залишків, а коваріація між ними відсутня, то матриця S має бути діагональною, а саме

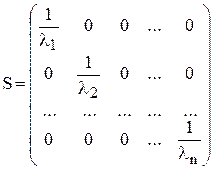(8.9)

За наявності гетероскедастичності для певних вихідних даних один або кілька факторів можуть різко змінюватися від одного спостереження до іншого, тоді як залежна змінна має такі самі коливання, як і для попередніх спостережень.

Це означає, що дисперсія залишків, яка змінюватиметься від одного спостереження до іншого (чи для групи спостережень), може бути пропорційною до величини фактора х (або до її квадрата), яка зумовлює гетероскедастичність, або пропорційною до квадрата залишків.

Звідси в матриці S значення λ_і можна обчислити:

а) у випадку 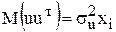, тобто коли дисперсія залишків пропорційна до зміни пояснювальної змінної х_і, то ;

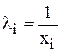б) у випадку, тобто коли дисперсія залишків пропорційна до зміни квадрата пояснювальної змінної, то ;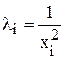

в) у випадку 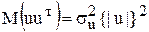, тобто коли дисперсія залишків пропорційна до зміни квадрата залишків за модулем, т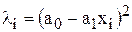о або .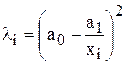

Оцінку параметрів вектора А згідно узагальненого методу найменших квадратів можна визначити за формулою:

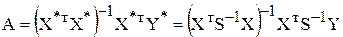(8.10)

При заданій матриці S оцінку параметрів моделі можна обчислити згідно з (8.10), тому можна скласти звичайні критерії значущості і довірчі інтервали.

8.4. Природа автокореляції та її тестування

Автокореляція відхилень – це кореляція відхилень від лінії регресії із відхиленнями від цієї лінії взятих із деякими запізненнями, тобто – це кореляція ряду u₁, u₂, u₃...u_n рядом u_1+k, u_2+k.. u_n, де k – це число, яке характеризує запізнення.

При k=1 існує кореляція між сусідніми членами ряду, яка називається автокореляцією першого порядку.

Автокореляція відхилень найчастіше спостерігається тоді, коли модель будується на основі часових рядів. Якщо існує кореляція між послідовними значеннями певного фактора, то буде спостерігатися і кореляція між послідовними значеннями відхилень.

Автокореляція може бути також наслідком помилкової специфікації моделі, крім того наявність автокореляції може означати, що до моделі необхідно ввести ще один фактор. Ще однією причиною виникнення автокореляції є те, що при дослідженні числові дані зібрані з великими похибками.

Якщо знехтувати автокореляцією відхилень і оцінити параметри моделі за методом МНК, то можливими є такі наслідки:

1. Оцінки параметрів моделі можуть бути не зміщеними, але неефективними.

2. Оскільки вибіркові дисперсії обчислюються не за уточненими формулами, то статистичні критерії t, F, які знайдено для моделі практично не можна використовувати.

3. Неефективність оцінок параметрів економетричної моделі призводить до неефективних прогнозів, тобто прогнозів з великою вибірковою дисперсією.

Перевірка наявності автокореляції можлива за певними критеріями.

1. Критерій Дарбіна – Уотсона.

Для оцінки автокореляції залишків найчастіше використовується критерій Дарбіна-Уотсона

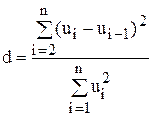, (8.11)

де - залишки (відхилення).

d – статистика може набувати будь-якого значення з інтервалу (0;4).

При відсутності автокореляції d – статистика набуває значень близьких до 2. Для d – статистики визначені крайні межі (d₁ – нижня, d_n – верхня), які дозволяють із заданою надійністю дати відповідь, чи можна прийняти гіпотезу про відсутність автокореляції першого порядку чи ні.

У залежності від значення d приймаємо, що:

1) при 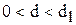відхилення додатньо корельовані;

2) при 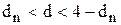враховується гіпотеза про відсутність явища автокореляції;

3) при 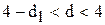відхилення від’ємно корельовані;

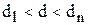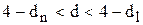4) при і критерій не дає відповідь про відсутність явища автокореляції.

Якщо d – статистика набуває значення з п. 4, то для одержання відповіді про наявність автокореляції першого порядку необхідно збільшити кількість спостережень. Величина d_n і d_l для певних ймовірностей наводяться в статистичних таблицях.

Між статистикою Дарбіна-Уотсона і коефіцієнтом автокореляції

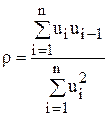(8.12)

існує приблизна залежність

.

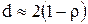При відсутності автокореляції 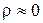, а d-статистика набуває значень, близьких до 2, при додатній автокореляції 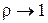, , 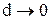а при від’ємній автокореляції , .

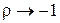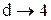2. Критерій фон Неймана.

Для виявлення автокореляції залишків можна використовувати критерій фон Неймана.

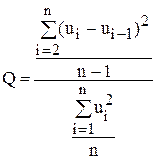(8.13)

Між критерієм Дарбіна–Уотсона і критерієм фон Неймана існує співвідношення.

(8.14)

При достатньо великих n→ ∞ ці критерії є однакові, тобто Q = d.

Фактичне значення критерію фон Неймана порівнюється з табличним для вибраного рівня ймовірності і заданій кількості спостережень. Якщо Q < Q_табл., то існує додатна автокореляція.

3. Циклічний коефіцієнт автокореляції

Цей коефіцієнт виражає ступінь взаємозв’язку рядів u_1,u_2,u_3.….u_n та u_2,u_3,u_4…..u_n,u_1.

Циклічний коефіцієнт кореляції визначають за формулою:

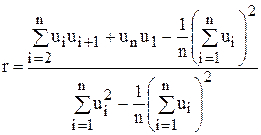(8.15)

Коефіцієнт r може набувати значень -1< r <1.

Від’ємні значеннясвідчать про від’ємну автокореляцію. Додатні – про додатну автокореляцію. Значення які містяться в області біля нуля свідчать про відсутність автокореляції.

В загальному випадку в обчисленні значення циклічного коефіцієнта автокореляції порівнюється з табличними для заданого рівня ймовірності і кількості спостережень.

Якщо |r| ≥ r_табл.,то існує автокореляція.

8.5. Оцінка параметрів регресійної моделі при наявності автокореляції.

Припустимо, що в економетричній моделі

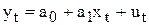(8.16)

де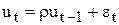

причому 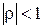, 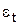- залишки, які розподілено нормально.

Щоб усунути автокореляцію залишків 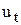треба перетворити модель (8.16) таким чином, щоб вона мала залишки .

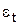Для оцінювання параметрів економетричної моделі, що має автокореляцію залишків можна використовувати узагальнений МНК, або метод Ейткена, який будується на скорегованій вхідній інформації з врахуванням коваріації залишків.

У п. 8.3 було розглянуто метод Ейткена і показано, що оцінку параметрів моделі можна визначити за формулою:

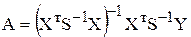(8.17)

де А- вектор оцінок параметрів,

Х - матриця значень факторів,

Y – вектор значень показника,

S – матриця для корегування вхідної інформації.

Отже, щоб оцінити параметри моделі на снові метода Ейткена, необхідно сформувати матрицю S. Вона буде мати вигляд:

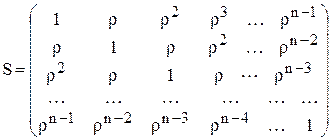(8.18)

У цій матриці 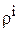виражає коефіцієнт автокореляції і-го порядку для залишків u. Коефіцієнт автокореляції 0-го порядку дорівнює 1.

Оскільк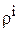и при 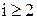часто наближаються до 0, то (8.18) можна записати у вигляді:

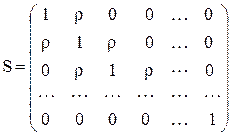(8.19)

а матриця, обернена до матриці S, буде мати вигляд:

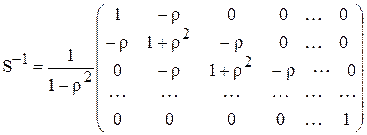(8.20)

Таку матрицю пропонується використовувати при оцінюванні параметрів економетричної моделі з автокорельованими залишками. Зауважимо, що параметр 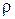має зміщення, тому використовуючи цей параметр для формування матриці S необхідно скорегувати його на величину зміщення:

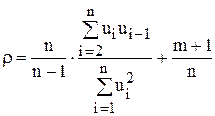(8.21)

де 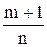- величина зміщення.

При реалізації алгоритму Ейткена при оцінці параметрів моделі використовують такі 5 кроків:

1. Оцінка параметрів моделі за допомогою МНК.

2. Дослідження відхилень на наявність автокореляції.

3. Формування матриці S.

4. Обертання матриці S.

5. Оцінка параметрів за допомогою методу Ейткена, тобто за формулою (8.17).

Дата добавления: 2014-01-04