Тема: виникнення і розвиток грошових відносин

Тема: Динаміка криволінійного руху матеріальної точки. Момент сили і момент імпульсу частинки. Рівняння моментів. Кінетична енергія при русі матеріальної точки по колу. Закон збереження моменту імпульсу.

Лекція №9.

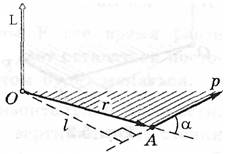Нехай частинка А, що має імпульс 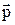, рухається по дузі кола навколо точки О. Положення точки характеризується радіус–вектором 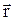, спрямованим до точки А з точки О.

Моментом імпульсу частинки А відносно точки О називають вектор 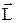, який дорівнює векторному добуткові векторів 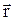і :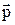

.

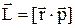Напрямок вектора 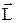обраний так, що обертання навколо точки О в напрямку вектора 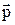і вектор 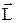утворять правогвинтову систему. Модуль вектора 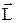дорівнює

,

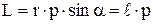де a – кут між векторами 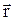і 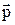, 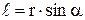– плече вектора 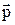відносно точки О.

З'ясуємо, яка механічна величина відповідальна за зміну вектора 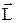в даній системі відліку. Для цього продифференціюємо формулу моменту імпульсу за часом:

.

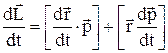Оскільки точка О нерухома, то вектор 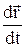дорівнює швидкості 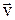частинки, тобто збігається по напрямку з вектором 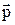, тому 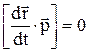. Відповідно до другого закону Ньютона 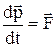, де 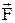– рівнодіюча всіх сил, які прикладені до частинки. Отже, .

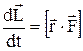Моментом сили 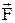відносно вісі обертання О називається векторна фізична величина, яка дорівнює векторному добуткові радіус–вектора і сили, що діє на точку:

.

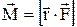Напрямок і модуль вектора 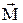визначається так само, як і :

,

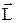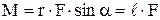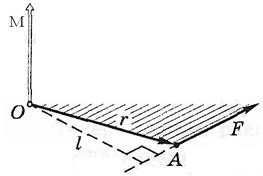де 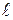– плече сили .

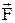Рівняння моментів: швидкість зміни моменту імпульсу 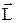частинки відносно деякої точки О обраної системи відліку дорівнює моменту 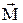рівнодіючої сили відносно тієї ж точки О:

.

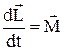Якщо система відліку є неінерціальною, то момент сили 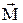містить у собі як момент сил взаємодії, так і момент сил інерції (щодо тієї ж точки О).

Момент імпульсу і момент сили відносно вісі

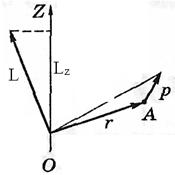Розглянемо в деякій системі відліку довільну нерухому вісь Z. Нехай відносно деякої точки О на осі Z момент імпульсу частинки А дорівнює 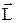, а момент сили, що діє на частинку, .

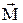Моментом імпульсу відносно осі Z називають проекцію на цю вісь вектора 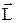, визначеного відносно довільної точки О даної вісі.

Моментом сили відносно осі Z називають проекцію на цю вісь вектора 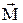, визначеного відносно довільної точки О даної вісі. Рівняння моментів у проекціях на вісь Z буде мати вигляд:

.

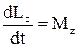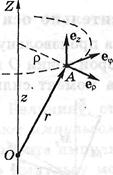
Знайдемо аналітичні вирази для проекцій моменту імпульсу і моменту сили. Для цього знайдемо проекцію на вісь Z векторних добутків 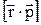і 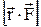. Скористаємося циліндричною системою координат r, j, z, зв'язавши з частинкою А орти 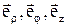, шо спрямовані убік зростання відповідних координат. У цій системі координат радіус–вектор 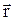і імпульс 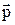частинки можна представити так:

, ,

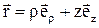
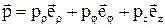де р_r, p_j, р_z – проекції вектора 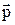на відповідні орти. З векторної алгебри відомо, що векторний добуток може бути представлено визначником:

, ,

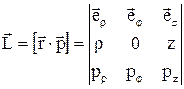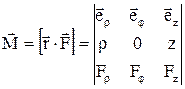відкіля одержуємо формули для проекцій моменту імпульсу і моменту сили на вісь Z:

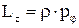и ,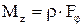

де r – найкоротша відстань частинки від осі Z. Оскільки проекція імпульсу частинки на орт 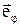дорівнює 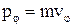, а 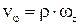, то в остаточному вигляді вираження для моменту імпульсу здобуває вигляд:

.

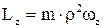Моментом інерції точки відносно довільної осі обертання називається фізична величина, що дорівнює добутку маси точки на квадрат найкоротшої відстані від осі обертання до лінії, уздовж якого спрямований вектор імпульсу:

.

З урахуванням останнього визначення формула для моменту імпульсу здобуває вигляд:

.

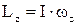Продифференціюємо останнє рівняння за часом:

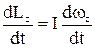або .

Отримане рівняння є другим законом Ньютона для обертального руху точки. У векторній формі воно має вигляд:

.

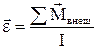Кінетична енергія при русі матеріальної точки по колу.

Нехай точка рухається по дузі кола навколо осі обертання зі швидкістю 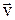. Кінетичну енергію в будь–який момент часу можна визначити а формулою:

.

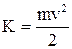Оскільки 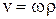, то після підстановки одержуємо: 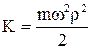. Але 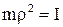. В остаточному підсумку формула кінетичної енергії обертального руху здобуває вигляд:

.

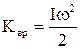Кінетичною енергією обертального руху називається фізична величина, яка дорівнює половині добутку моменту інерції на квадрат кутової швидкості.

Закон збереження моменту імпульсу.

Нехай система складається з деякої довільної кількості частинок.

Моментом імпульсу системи називають векторну суму моментів імпульсів окремих її частинок: 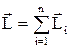, де усі вектори визначені відносно однієї і тієї ж точки О заданої системи відліку. Представимо момент усіх сил, що діють на частинки системи у вигляді суми моментів зовнішніх і внутрішніх сил. Тоді основне рівняння динаміки для обертального руху буде мати вигляд:

.

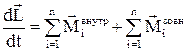Але за третім законом Ньютона моменти внутрішніх сил попарно компенсуються, тому сумарний момент усіх внутрішніх сил дорівнює нулю. У підсумку останнє рівняння здобуває вигляд:

.

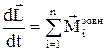З отриманого рівняння випливає: .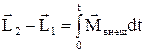

Висновок: збільшення моменту імпульсу системи за кінцевий проміжок часу дорівнює імпульсу сумарного моменту всіх зовнішніх сил за відповідний проміжок часу.

Закон збереження моменту імпульсу: у замкнутій системі момент імпульсу системи частинок не змінюється:

.

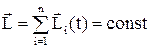План:

1. Виникнення і розвиток грошових відносин.

2. Сутність грошей.

3. Еволюція форм грошей.

Мета: 1. навчальна – ознайомити студентів з різними концепціями виникнення і розвитку грошових відносин, сутністю і основними властивостями грошей та еволюцією їх форм.

2. розвивальна – розвивати у студентів творчу думку, нестандартне мислення, інтелектуальні здібності, професійну та термінологічну мову, уміння і навички.

3. виховна – виховувати економічне мислення, толерантність, плюралізм думок, поважне ставлення до думки іншого, професійні та соціально-значущі якості особистості.

Дата добавления: 2014-01-04