Характеристика генетичних операцій і основних етапів роботи ГА

Хотілося б відзначити, що ГА є досить ефективним і разом з тим досить складним інструментом для рішення великого класу задач, внаслідок чого сам ГА вимагає досить тонкого й склад­ного настроювання. При рішенні прикладних задачь у кожному конкретному випадку можливе використання ГА з досить спе­цифічними особливостями, що полягають в обраному дослідни­ком наборі генетичних операцій, порядку застосування цих опе­рацій, значенні власних параметрів ГА й ряду інших характерис­тик.

При конкретній практичній реалізації ГА його структурна схема може абсолютно не збігатися зі схемою на рисунок 9.3. Процес синтезу структури ГА є ітераційним.

а) кодування

Кодування як автоматична операція в процесі роботи ГА не виконується (!) – це один з найбільш важливих попередніх, творчих процесів здійснюваних дослідником (інженером) при проектуванні роботи ГА.

Даний етап припускає визначення способу компонування, побудови хромосоми, способу пред­ставлення в ній інформації.

Від якості рішення задачі коду­вання принципово залежить ефективність роботи ГА, аж до можливості рішення задачі взагалі.

Таблиця 9.2

Дешифрування фрагментів хромосом

Код Гріючи	Двійково–де­сятковий код	Десяткове значення зру­шення

Процедура кодування дозволяє перейти від фенотипу до генотипу, тобто представити набір шуканих змінних у вигляді деякого закодованого рядка – хромосоми. Найбільш широке поширення при використанні ГА одержало двійкове коду­вання з використанням 0 і 1. Перевагою даного способу є про­стота, природність і висока ефективність застосування генети­чних операцій. Відносно широке поши­рення одержав спосіб подання інформації в хромосомі у деся­тковій системі числення. Даний підхід дозволяє зекономити частину обчислювальних ресурсів при декодуванні генотипу у фенотип (тому що не вимагає перерахування значень парамет­рів з однієї системи числення в іншу). Крім того в деяких ви­падках доцільно використовувати підхід до кодування інфор­мації з використанням алфавіту з 3–ех елементів: 1, 0 і #, де # – означає, що на даній позиції може бути як 1 так і 0, тобто зна­чення цієї позиції не істотно для фенотипу. Використання ін­ших видів кодування знайшло менш широке вживання.

При використанні двійкового кодування в ГА необхідно використати не двійково–десятковий код, а спеціальний код Грєя (таб. 9.2).

Крім вибору коду для подання інформації варто звернути увагу на наступні моменти:

1. Більш творчо ставитись до вибору змісту шуканого па­раметра, який кодується – це може бути не просто значення деякого параметра системи: у деяких випадках це може бути номер певної операції, при визначенні оптимального ланцю­жка операцій; це може бути фіксована назва деякої змінної, а значима інформація може бути в положенні гена в хромосомі; це може бути вага деякого правила при настроюванні бази знань; при генетичному (еволюційному) програмуванні це можуть бути змінні, константи, операції й навіть окремі функ­ції й процедури тощо.

2. Визначившись зі змістом параметра, який кодується ко­жним геном необхідно чітко визначити алельний алфавіт, тобто перелік всіх можливих припустимих значень гена. Ін­шими словами необхідно визначити перелік тих значень генів які при декодуванні не втратять сенс у рамках розв'язуваної задачі.

3. При компонуванні хромосоми гени відповідальні за ко­дування параметрів однієї й тієї ж підсистеми (підзадачі) по­винні бути розташовані максимально близько одна від іншої. Чим сильніше взаємозалежні підсистеми (підзадачі) одна від іншої, тим ближче повинні бути розташовані гени в хромосомі відповідальні за кодування параметрів цих підсистем (підза­дач).

4. Будь–яка інформація в ГА представляється по суті в дис­кретному виді (таб. 9.2). В зв’язку з чим при кодуванні необ­хідно вибрати таку розмірність коду для кожного гена, якаб забезпечила перекриття динамічного діапазону параметра, що кодується з необхідною точністю, що буде визначатись ціною однієї дискрети.

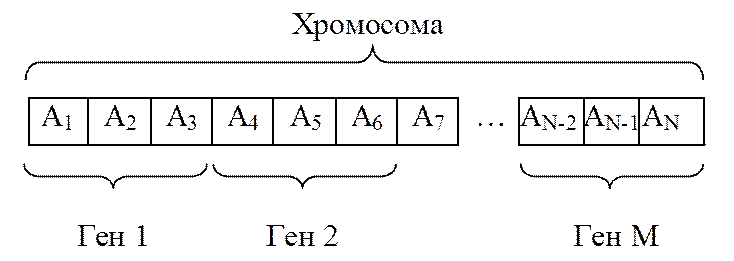
Рисунок 9.4 – Приклад хромосоми

При розгляді інших етапів і операцій для прикладів будемо використовувати хромосоми із двійковим кодуванням. Будемо вважати, що кожна змінна Xj кодується певним фрагментом хромосоми – геном (див. рисунок 9.4). У будь–якій позиції хро­мосоми може стояти як нуль, так і одиниця. Розташовані по­руч фрагменти не відокремлюють один від одного якими–не­будь маркерами, проте, при декодуванні хромосоми протягом усього періоду моделювання еволюційного процесу викорис­товується одна й та сама маска розташування генів.

Згадаємо про деякі менш розповсюджені способи кодування й подання інформації в хромосомі.

В [7-13] описується диплоідний спосіб кодування інформації в хромосомі, що в природних умовах відповідає статевому спо­собу розмноження і є більше досконалим способом відтворення потомства. Раніше ми розглядали гаплоідний спосіб кодування при якому генотип однозначно відповідає фенотипу. При дип­лоідному кодуванні немає однозначного зв'язку між фенотипом і генотипом. Алельний алфавіт при бінарному кодуванні склада­ється з 4 символів: А – домінантної одиниці, а – рецесивної одиниці, В – домінантного нуля, b – рецесивного нуля. Кожна особина (генотип) складається з 2–х батьківських хромосом. Де­кодування виробляється у два етапи. Спершу із двох хромосом з урахуванням ознак домінантності–рецесивності формується бі­нарний рядок згідно таблиці 9.3. Після чого бінарний рядок де­кодуєтся в вектор параметрів як при гаплоідному кодуванні.

Таблиця 9.3 – Таблиця декодування при диплоідному кодуванні інформації в ГА

Хромосома 1	Хромосома 2	Бінарний рядок
А	А
А	а
а	А
a	a
B	B
B	b
b	B
b	b
A	B
A	b
B	a
b	a

Диплоідний спосіб кодування вимагає додаткових ресурсів при його моделюванні, крім того ГА з таким способом коду­вання, як правило, має гіршу швидкість збіжності (у порівнянні з гаплоідним способом кодування), однак дозволяє більш рете­льно досліджувати простір пошуку й з меншою ймовірністю «застряє» у локальних екстремумах, що особливо важливе при нестаціонарній цільовій функції. Розглянутий варіант кодування інформації в ГА в більшій мірі схожий із природними проце­сами, однак і він є істотним спрощенням цих процесів.

Висновок: Вибір способу кодування визначає при­пустимий перелік і різновид операцій зміни (схрещування, мута­ції, інверсії).

б) формування початкової (вихідної) популяції

Хромосоми генеруються випадковим чином (за рівномір­ним законом розподілу ймовірності), шляхом послідовного заповнення розрядів (генів), відразу в бінарному вигляді, і всякі наступні зміни в популяції зачепають спочатку генети­чний рівень, а тільки потім аналізуються фенотипічні нас­лідки цих змін, але ніколи не навпаки. Можливо, якщо апрі­орно відомі деякі характеристики простору пошуку, вихідна популяція може формуватися не за рівномірним законом, а по нормальному з урахуванням відомих околиць екстрему­мів, хоча це в деякому розумінні суперечить ідеям еволю­ційних обчислень.

Величина популяції (тобто кількість хромосом) – один з найважливіших параметрів при практичному використанні ГА. У випадку занадто малої величини популяції відносно швидко відбувається збіжність ГА до локального оптимуму. У противному випадку затрачаються більші обчислювальні ресурси й час очікування поліпшення результатів може бути дуже тривалим. Розмір популяції може бути фіксованої й змінної довжини.

Існують ГА, у яких одночасно можуть існувати не одна, а відразу кілька популяцій. При цьому обов'язково передбача­ється спеціальний механізм, що визначає порядок взаємодії особин з різних популяцій між собою (через фіксовану кіль­кість епох, через фіксований проміжок часу, при досягненні певного значення функції пристосованості, при досягненні певного поліпшення функції пристосованості, при певному взаємному положенні хромосом у просторі пошуку; випад­кові хромосоми, тільки кращі, тільки гірші, кращі хромо­соми з однієї популяції й гірші з інший і т.п.). Кожній попу­ляції може приділятися різна роль: популяції можуть бути приблизно однаковими по своїх характеристиках і призна­ченню, або ж використовуватись для різних цілей (напри­клад, одна популяція – для дослідження простору пошуку, інша – для поліпшення рішень в околицях локальних екстре­мумів).

в) відбір

Етап відбору в ГА припускає здійснення вибору для пода­льшого використання частини хромосом з популяції (або якщо подивитися на це з іншого боку – це етап відсівання, відкидання менш ефективних хромосом). Даний етап включає операції де­кодування, оцінки (обчислення функції пристосованості) і власне вибору.

г) декодування

Дана операція передбачає перетворення зворотні кодуванню, тобто перехід від генотипу до фенотипу (таб.1), що необхідно для обчислення значення функції пристосованості.

д) оцінка

Етап оцінки – етап обчислення ФП. Необхідно підкреслити, що в генетичному алгоритмі лише одна деталь має прив'язку до конкретної розв'язуваної завдачі – це функція пристосова­ності. Інші оператори можуть бути вільно перенесені для рі­шення інших задач без змін і в будь–яких комбінаціях.

Спосіб обчислення ФП у значній мірі визначається способом кодування (мається на увазі не вид коду: двійковий або десятко­вий, а спосіб компонування хромосоми, сенс значення гена й т.п.).

При визначенні ФП потрібно виділити наступні головні мо­менти:

1. ФП повинні бути адекватні задачі, яка вирішується. Це означає, що для успішного пошуку необхідно, щоб розподіл значень ФП збігались з розподілом реальної якості рішень (не завжди "якість" рішення еквівалентна його оцінці по ФП). Простіше кажучи, ФП завжди повинна прагнути задовольнити умові: для всіх рішень X виконується F(X1)<F(X2) при K(X1)<K(X2), де K(X) – реальна якість рішення, а F(X) – його оцінка по ФП.

2. ФП повинна мати рельєф. Більш того, рельєф повинен бути різноманітним. Це означає, що ГА має мало шансів на успіх, якщо на поверхні ФП є величезні "плоскі" ділянки. Це призводить до того, що багато рішень в популяції (або, що гі­рше – усі рішення) при розходженні в генотипі будуть мати однакове значення ФП, алгоритм не буде мати можливості виб­рати краще рішення, вибрати напрямок подальшого розвитку.

3. Обчислення ФП повинне вимагати мінімум ресурсів. Так, як ця деталь алгоритму найбільш часто використовується, шви­дкість її обчислення має істотний вплив на швидкість роботи алгоритму в цілому.

4. Для виключення передчасної збіжності ГА до локального екстремуму, значення ФП необхідно масштабувати.

Масштабування проводиться для забезпе­чення відповідного рівня конкуренції хромосом під час репроду­кції. У випадку відсутності масштабування проявляється праг­нення до домінування в процесі селекції з боку невеликої кіль­кості «суперіндивідів». У такій ситуації значення ФП повинні бути зменшені, щоб уникнути домінування в популяції. Найбільш часто за­стосовуються наступні методи масштабування: лінійне масшта­бування, σ– відрізання, і ступеневе масштабування.

При лінійному масштабуванні модифіковану ФП отриму­ють із початкової f, застосовуючи лінійне перетворення виду , де a, b – коефіцієнти лінійного перетворення. Ці коефіцієнти варто підбирати таким чином, щоб були виконані умови:

1. Незмінність середнього значення ФП у популяції.

2. Максимальне значення промасштабованої ФП повинне бути на рівні певної кратності середнього пристосування.

У методі σ– відрізання, 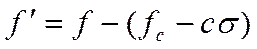, де с – кратність, рі­вна 1–З, 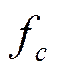– середнє значення f по популяції.

Ступеневе масштабування пов'язане зі зведенням вихідної ФП у деякий ступінь: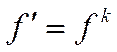, де k – масштабний коефіцієнт.

Приведемо приклад визначення значення ФП, для випадку рішення завдання класифікації. Значення ФП для конкретної хромосоми, у цьому випадку визначається як відношення кіль­кості правильних відповідей до загальної кількості прикладів, які застосовувались при навчанні.

Також на даному етапі з подальшого розгляду виключаються хромосоми з неприпустимим (не маючим сенсу) значенням але­лей.

Дата добавления: 2014-01-04