Линейное уравнение переноса

Уравнение переноса

Лекция №10

Вспомогательные расчеты для определения параметров ряда Фурье

Моделирование сезонных колебаний товарооборота

Месяц	t	yt	cos t	sint	y*cost	y*sint	yt (расчет)
Январь		27,3	1,0000	0,0000	27,300	0,000	30,14
Февраль	π/6		0,8660	0,5000	24,249	14,000	29,53
Март	π/3	31,2	0,5000	0,8660	15,600	27,020	29,20
Апрель	π/2	30,1	0,0000	1,0000	0,000	30,100	29,22
Май	2π/3	29,2	-0,5000	0,8660	-14,600	25,288	29,59
Июнь	5π/6		-0,8660	0,5000	-25,981	15,000	30,21
Июль	π	30,1	-1,0000	0,0000	-30,100	0,000	30,91
Август	7π/6		-0,8660	-0,5000	-27,713	-16,000	31,52
Сентябрь	4π/3	31,4	-0,5000	-0,8660	-15,700	-27,193	31,85
Октябрь	3π/2	32,3	0,0000	-1,0000	0,000	-32,300	31,83
Ноябрь	5π/3	31,2	0,5000	-0,8660	15,600	-27,020	31,46
Декабрь	11π/6	33,5	0,8660	-0,5000	29,012	-16,750	30,84
		366,3			-2,333	-7,855	366,30

На основе сумм, рассчитанных в последней строке таблицы, рассчитываются параметры a₀ = 30,53; a₁ =-0,39; a₂=-1,31. В последнем столбце находятся расчетные значения исходного ряда.

Рассмотрим еще один пример моделирования циклических колебаний.

Пример. Предполагая наличие циклических колебаний, проведем гармонический анализ динамики отклонений от линейного тренда данных о ставках по кредитам за 12 месяцев (у_t — ŷ_t).

Исходные данные для расчета приведены в таблице 9.7.

Рассчитаем первую гармонику. Для определения значений синусов и косинусов необходимо использовать таблицу вычисления значений по ряду Фурье.

Исходя из определенных значений синусов и косинусов для каждого уровня ряда динамики (графы 4 и 5 таблицы 4.3) рассчитаем параметры а₀, a₁ и b₁:

a₀ = 0; a₁ = 125,6 / 6 = 20,9; b₁ = - 63,5 / 6 = - 10,6.

Таблица 9.7.

Месяц	уt — ŷt	t	cos t	sin t	yt cos t	yt sin t	ŷt
I	52,5		1,0000	0,0000	52,5		20,9
II	- 50	π /6	0,8660	0,5000	-43,3	- 25	12,8
Ш	12,5	π /3	0,5000	0,8660	6,3	10,8	1,3
IV	-2,5	π /2	0,0000	1,0000		-2,5	-10,6
У		2 π /3	-0,5000	0,8660	- 35	60,6	-19,6
VI	-62,5	5 π /6	-0,8660	0,5000	54,1	-31,3	-23,4
VII	-77,5	π	-1,0000	0,0000	77,5		-20,9
VIII	- 50	7 π /6	-0,8660	-0,5000	43,3		-12,8
IХ		4 π /3	-0,5000	-0,8660	-42,5	-73,6	-1,3
X	- 15	З π /2	0,0000	-1,0000			10,6
XI		5 π /3	0,5000	-0,8660	32,5	-56,3	19,6
XII	-27,5	11 π /6	0,8660	-0,5000	-23,8	13,8	23,4
Итого:					125,6	-63,5

Таким образом, первая гармоника описывается уравнением:

у = 20,3 sin t -10,6 cos t

Аналогично производится расчет гармоник второго и высших порядков.

Их значения последовательно присоединяются к значениям первой гармоники.

Далее, подставляем в уравнение соответствующие значения t= π /6, π/3… и т.д. В результате этих расчетов получаем выравненные уровни отклонений процентных ставок от их средней величины.

Вычислив остаточные дисперсии для гармоник, можно определить, какая гармоника ряда Фурье максимально приближена к эмпирическим данным, т.е. какая гармоника наиболее точно характеризует циклические колебания процентных ставок

После нанесения ординат синусоидально-косинусоидальной функции на график можно получить наглядное представление о широте амплитуды, характере и продолжительности цикла, определить его начало и окончание.

Заключение. На данной лекции были подробно рассмотрены различные способы анализа структуры временного ряда, моделирования сезонных и циклических колебаний. На следующей лекции мы рассмотрим проблемы оценки взаимосвязей временных рядов.

Задачи описания переноса частиц в веществе весьма разнообразны: это перенос электронов, протонов и нейтронов, перенос гамма излучения, диффузия одного вещества в другом, конвективный перенос в жидкости и в газе и прочие задачи. Задачи подобного типа могут быть сведены к решению нелинейных интегро-дифференциальных уравнений. Например, кинетическая теория газов базируется на уравнении Больцмана, которое имеет следующий вид:

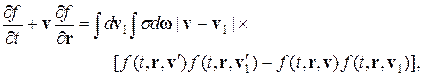(1)

где 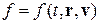— функция распределения газа атомов, скорости пары атомов до и после взаимодействия с дифференциальным сечением (d w = 2 p sin c dc — телесный угол, где c — угол отклонения при взаимодействии пары атомов) удовлетворяют законам сохранения импульса и энергии:

Решение уравнения Больцмана (1) крайне сложно и выходит за пределы данного курса лекций. Ограничимся решением линейного дифференциального уравнения вида:

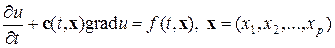, (2)

где c — вектор скорости переноса. Многомерность уравнения переноса (2) не вносит ничего принципиально нового, поэтому в дальнейшем будем исследовать одномерное уравнение переноса с постоянной, если не оговорено противное, скоростью c:

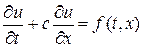. (3)

Если правая часть уравнения (3) равна нулю, уравнение можно решить в общем виде, тогда решение выступает в форме бегущей волны

, (4)

где f = f (x) — произвольная функция. Согласно (4) видно, что параметр c выступает в качестве скорости переноса, причем при c > 0 волна двигается слева направо. Учитывая (4), определим типичные корректные постановки задачи решения уравнения переноса (3).

Смешанная задача Коши. Зададим начальные и граничные условия вида:

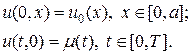(5)

Решение задачи (3), (5) однозначно определено в области G (t, x) = [0, T ] ´ [0, a ], если начальное и граничное условия непрерывны вместе со своими p -и производными, при этом выполнены условия согласования в точке стыка начальных и граничных условий. Для случая f (t, x) = 0 условия стыковки имеют вид:

,

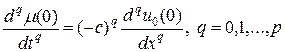которое следует из точного решения задачи (3), (5):

(6)

Для случая, когда f (t, x) непрерывна вместе с (p -1)-й производной, то решение u (t, x) непрерывно в G вместе с p -й производной.

Задача Коши. Определим начальные данные на полубесконечной прямой: 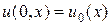, x Î (-¥, a ]. В этом случае решение однозначно определено в области G (t, x) = [0,+¥) ´ (-¥, a ]. Гладкость решения соответствует гладкости начального данного и правой части f (t, x).

Характеристики уравнения (3) имеют вид x - ct = const и являются прямыми линиями при c = const. Решение (4) однородного уравнения (3) постоянно вдоль характеристики, поэтому говорят, что начальные и граничные условия переносятся вдоль характеристик. На рис.1 приведена иллюстрация такого переноса на примере решения (6). Точка стыка начального и граничного условий развернутая во времени является характеристикой, которая представлена на рис.1 красной стрелкой.

Рис.1. Перенос начального и граничного условия уравнения
переноса по характеристикам

Рассмотрим разностные схемы решения смешанной задачи Коши. Они называются схемами бегущего счета. Схемы бегущего счета легко обобщаются на многомерный случай, они просты и позволяют решать уравнения переноса с различного рода усложнениями.

Для решения задачи (3), (5) в области G (t, x) = [0, T ] ´ [0, a ] введем равномерную для простоты сетку с шагами t и h по времени и пространству соответственно. Рассмотрим четыре расчетных шаблона, представленных на рис.2.

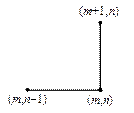
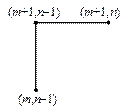
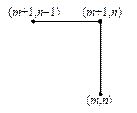
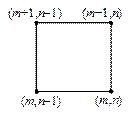
Рис.2,а. Трехточечный шаблон	Рис.2,б. Трехточечный шаблон	Рис.2,в. Трехточечный шаблон	Рис.2,г. Четырехточечный шаблон

Составим разностные схемы ко всем четырем шаблонам на рис.2.

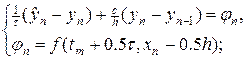(7а)

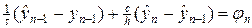, (7б)

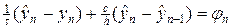, (7в)

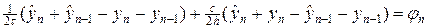. (7г)

Во всех четырех схемах правая часть выбиралась в центре ячейки. Возможен и другой способ аппроксимации правой части.

Все четыре разностные схемы (7а) — (7г), по существу, являются явными. Во всех схемах значение явно выражается через 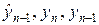. Решение на нулевом слое известно из начального условия, т.е. 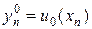. Для вычисления решения на следующем слое из граничного условия находим 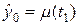, это позволяет найти 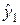, далее вычисляется 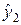и т.д. Таким образом находится решение на первом слое, аналогично находится решение на втором слое и т.д. Именно в связи с тем, что решение вычисляется слой за слоем слева направо, схемы (7а) — (7г) называются схемами бегущего счета.

Алгоритмы бегущего счета обеспечивают существование и единственность решений при любых 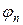. Поэтому для доказательства сходимости остается разобраться с аппроксимацией и устойчивостью разностных схем. Поскольку граничное условие воспроизводится точно, постольку исследование устойчивости по нему не требуется.

Разностная схема (7а). Исследуем погрешность аппроксимации схемы (7а). Для этого разложим решение и правую часть в окрестности точки (t_m, x_n) в ряд Тейлора, считая непрерывность всех требуемых производных:

,

,

.

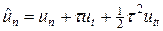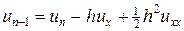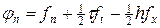Учитывая эти разложения, находим невязку схемы (7а):

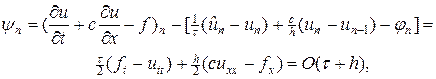
т.е. схема (7а) имеет аппроксимацию первого порядка в норме .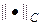

Устойчивость исследуем с помощью принципа максимума, формулировка и доказательство которого приведены в лекции №9. Критерий равномерной устойчивости по начальным данным (формула (64) в лекции №9 при C = 0) дает следующее ограничение:

,

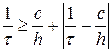которое сводится к так называемому условию Куранта

ct £ h. (8)

Согласно (8), разностная схема (7а) является условно устойчивой© в норме .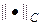

Методом разделения переменных можно доказать необходимость условия (8) для обеспечения устойчивости. Подставим в схему (7а) следующие величины:

,

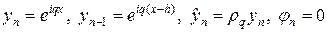тогда множитель роста гармоники

.

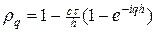Условие устойчивости 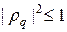обеспечивается, когда

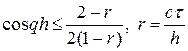. (9)

Выполнение неравенства (9) при произвольном q обеспечено, когда r £ 1, т.е. при выполнении условия Куранта. При нарушении условия Куранта, т.е. при r > 1 неравенство (9) не выполняется при всех q, а только при некоторых. Так, при r >> 1 неравенство (9) перепишется в виде: cos qh £ ½, т.е. амплитуды некоторых гармоник растут при переходе со слоя на слой и схема неустойчива по начальным данным.

Устойчивость по правой части согласно формуле (65) лекции №9 обеспечивается при k = 1 в норме 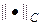, когда верно условие Куранта.

В итоге схема (7а) при выполнении условия Куранта сходится в 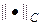с первым порядком точности.

В качестве примера рассмотрим численное решение задачи

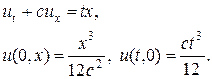(10)

Задача (10) имеет следующее аналитическое решение:

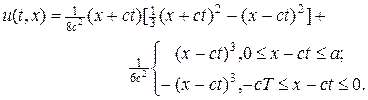(11)

На листинге_№1 приведен код программы численного решения задачи (10) по разностной схеме (7а). На рис.3,а приведено трехмерное изображение решения u (t, x) при выполнении условия Куранта, а на рис.3,б приведено решение при нарушении условия Куранта. Видно, появление неустойчивости в решении при нарушении условия (8).

Листинг_№1

%Программа численного решения уравнения

%переноса du/dt+cdu/dx=tx

%u(0,x)=x^3/(12c^2), u(t,0)=(ct^3)/12

%очищаем рабочее пространство

clear all

%определяем параметр скорости переноса c,

%а также отрезок времени интегрирования T и

%диапазон изменения пространственной

%переменной a

c=0.25; T=2; a=1;

%определяем шаг по пространству

h=0.005;

%рассматривается два варианта расчета

%при tau=h/c (условие Куранта выполняется) и

%при tau=1.12*h/c (условие Куранта нарушено)

tau=(1.0*h)/c;

r=(c*tau)/h;

%определяем сетки по времени и по пространству

t=0:tau:T;

x=0:h:a;

%определяем начальное значение u(0,x)=x^3/(12c^2)

for j=1:length(x)

y(1,j)=x(j)^3/(12*c^2);

end

%организуем расчет по разностной схеме (7а)

for i=1:(length(t)-1)

%определяем левое граничное значение

%u(t,0)=(ct^3)/12

y(i+1,1)=(c*t(i+1)^3)/12;

for j=2:length(x)

y(i+1,j)=(1-r)*y(i,j)+r*y(i,j-1)+...

tau*(t(i)+0.5*tau)*(x(j)-0.5*h);

end

end

[xi ti]=meshgrid(x,t);

%рисуем численное решение уравнения переноса u(t,x)

surf(ti,xi,y); [xi ti]=meshgrid(x,t);

%рисуем численное решение уравнения переноса u(t,x)

surf(ti,xi,y);

Рис.3,а. Численное решение уравнения (10) по разностной схеме (7а) при выполнении условия Куранта	Рис.3,б. Численное решение уравнения (10) по разностной схеме (7а) с нарушением условия Куранта (8)

Сравним теперь численное решение задачи (10) и аналитическое решение (11). На листинге_№2 приведен код соответствующей программы. В программе считается, что t = 0.5 h/c и варьируется шаг по пространству. На рис.4 приведен итог работы кода программы листинга_№2 в виде кривой зависимости отношения ошибки численного решения к шагу сетки const(h) = 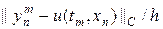в зависимости от шага сетки h. Из условия аппроксимации разностной схемой (7а) исходного уравнения (3) с порядком O (t + h) следует, что величина const(h) должна стремиться к некоторой константе по мере того, как h ® 0. Такая тенденция видна на рис.4.

Листинг_№2

%Программа численного решения уравнения

%переноса du/dt+cdu/dx=tx

%u(0,x)=x^3/(12c^2), u(t,0)=(ct^3)/12 и

%сравнение его с аналитическим решением

function schm1_conv

global c

%определяем параметр скорости переноса c,

%а также отрезок времени интегрирования T и

%диапазон изменения пространственной

%переменной a

c=0.25; T=2; a=1; h=0.2;

%определяем количество делений шага h пополам

kmax=7;

for k=1:kmax

%делим шаг h пополам

h=h/2;

%определяем шаг по времени, который считается

%пропорциональным шагу по пространству

tau=0.5*h/c; r=(c*tau)/h;

%определяем сетки по времени и по пространству

t=0:tau:T; x=0:h:a;

%определяем начальное значение u(0,x)=x^3/(12c^2)

for j=1:length(x)

y(1,j)=x(j)^3/(12*c^2);

end

%организуем расчет по разностной схеме (7а)

for i=1:(length(t)-1)

%определяем левое граничное значение

%u(t,0)=(ct^3)/12

y(i+1,1)=(c*t(i+1)^3)/12;

for j=2:length(x)

y(i+1,j)=(1-r)*y(i,j)+r*y(i,j-1)+...

tau*(t(i)+0.5*tau)*(x(j)-0.5*h);

end

end

for i=1:length(t)

for j=1:length(x)

yt(i,j)=abs(y(i,j)-ya(t(i),x(j)));

end

end

step(k)=h;

%определяем ошибку численного решения в норме C

%и делим ее на шаг сетки h

const(k)=max(max(yt))/h;

end

%рисуем зависимость предстепенной константы от

%шага сетки h

plot(step,const,'-*','MarkerSize',12);

%функция, возвращающая аналитическое решение

function z=ya(t,x)

global c

z=(1/(8*c^2))*(x+c*t)*((x+c*t)^2/3-(x-c*t)^2);

if (x-c*t)>=0

z=z+(x-c*t)^3/(6*c^2);

else

z=z-(x-c*t)^3/(6*c^2);

end

Разностная схема (7б) исследуется аналогично. Для исследования аппроксимации разложение в ряд Тейлора удобно проводить в окрестности узла (x_{n -1}, t_m + t). Для дважды непрерывно дифференцируемого решения данная схема при выполнении условия устойчивости

ct ³ h (12)

обеспечивает сходимость со скоростью O (t + h).

Разностная схема (7в) безусловно устойчива и на дважды непрерывно дифференцируемых решениях сходится к точному решению со скоростью O (t + h).

Разностная схема (7г) симметричная и следует ожидать, что порядок ее аппроксимации выше, чем в предыдущих членах. Для оценки порядка аппроксимации разложение в ряд Тейлора удобно провести в окрестности центра ячейки 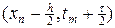. После проведения соответствующих выкладок, можно найти оценку невязки:

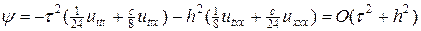. (13)

Тем самым схема (7г) имеет второй порядок аппроксимации, когда решения имеют непрерывные производные вплоть до третьей.

Рис.4. Зависимость предстепенной константы в оценке ошибки
численного решения от шага сетки

Устойчивость разностной схемы (7г) исследуем с помощью метода разделения переменных. Подставляя в (7г)

,

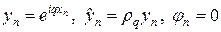найдем значение коэффициента роста Фурье-гармоники при переходе со слоя на слой:

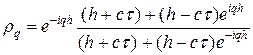. (14)

Из оценки (14) следует, что 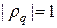для любой гармоники и при любых соотношениях шагов. Это означает, что схема (7г) безусловно и равномерно устойчива по начальным данным в норме .

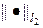Исследуем разностную схему (7г) на предмет сходимости в двух нормах: 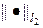и 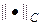. На листинге_№3 приведен код программы для изучения сходимости схемы (7г) на примере численного решения задачи (10) и сравнения полученного решения с аналитическим решением (11). В программе вычисляются зависимости предстепенных констант const(h) для двух норм от шага сетки h, при этом считается, что t = 0.5 h / c. Согласно теоретическим оценками, предстепенная константа const(h) = 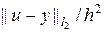должна выходить на некоторое постоянное значение при h ® 0.

Листинг_№3

%Программа численного решения уравнения

%переноса du/dt+cdu/dx=tx

%u(0,x)=x^3/(12c^2), u(t,0)=(ct^3)/12 и

%сравнение его с аналитическим решением

function schm4_conv

global c

%определяем параметр скорости переноса c,

%а также отрезок времени интегрирования T и

%диапазон изменения пространственной

%переменной a

c=0.25; T=2; a=1; h=0.2;

%определяем количество делений шага h пополам

kmax=7;

for k=1:kmax

%делим шаг h пополам

h=h/2;

%определяем шаг по времени, который считается

%пропорциональным шагу по пространству

tau=0.5*h/c; r=(c*tau)/h;

%определяем сетки по времени и по пространству

t=0:tau:T; x=0:h:a;

%определяем начальное значение u(0,x)=x^3/(12c^2)

for j=1:length(x)

y(1,j)=x(j)^3/(12*c^2);

end

%организуем расчет по разностной схеме (7г)

for i=1:(length(t)-1)

%определяем левое граничное значение

%u(t,0)=(ct^3)/12

y(i+1,1)=(c*t(i+1)^3)/12;

for j=2:length(x)

y(i+1,j)=((r-1)/(r+1))*...

(y(i+1,j-1)-y(i,j))+y(i,j-1)+...

2*(tau/(r+1))*(t(i)+0.5*tau)*(x(j)-0.5*h);

end

end

for i=1:length(t)

for j=1:length(x)

yt(i,j)=abs(y(i,j)-ya(t(i),x(j)));

end

end

s=0;

for i=2:(length(t)-1)

for j=2:(length(x)-1)

s=s+tau*h*(y(i,j)-ya(t(i),x(j)))^2;

end

end

step(k)=h;

%оцениваем ошибку численного решения в нормах

%l2 и C и делим эти оценки на квадрат шага h^2

constl2(k)=max(max(yt))/h^2;

constC(k)=sqrt(s)/h^2;

end

%рисуем зависимость предстепенной константы в

%оценке ошибки от шага сетки h

plot(step,constl2,'-*',step,constC,'-p','MarkerSize',12);

%функция, возвращающая аналитическое решение

function z=ya(t,x)

global c

z=(1/(8*c^2))*(x+c*t)*((x+c*t)^2/3-(x-c*t)^2);

if (x-c*t)>=0

z=z+(x-c*t)^3/(6*c^2);

else

z=z-(x-c*t)^3/(6*c^2);

end

На рис.5 приведен итог работы программы листинга_№3. Отчетливо видно, что и в норме 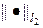, и в норме 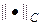численное решение по разностной схеме (7г) сходится к аналитическому решению со вторым порядком точности по t и h.

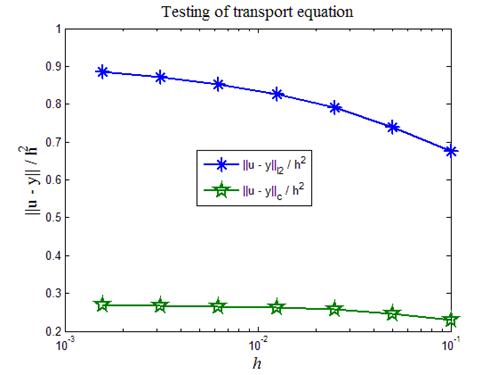
Рис.5. Зависимости предстепенных констант в оценках ошибок
численного решения для двух норм

Дата добавления: 2014-01-04