Лекция 10. Аппроксимация функции. Пример

В качестве примера рассмотрим исходные данные, с которыми мы работали для нахождения интерполяционного полинома методом Ньютона.

Таблица

y
x	3.5		2.5		1.5

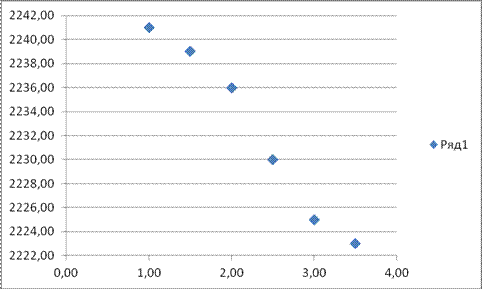
В качестве примера я не стала брать сотни значений, хотя, если будет такая практическая необходимость, это не сильно усложнит расчеты – нужно будет найти их сумму, сумму их квадратов и т.п., но получена будет все равно система из 2 уравнений, как и в нашем случае.

Предположим, что зависимость является линейной. В качестве аппроксимирующего многочлена выберем многочлен первой степени вида:

.

Тогда 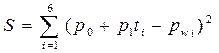. Система линейных уравнений для поиска параметров будет иметь следующий вид:

,

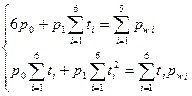где значения коэффициентов при неизвестных параметрах равны:

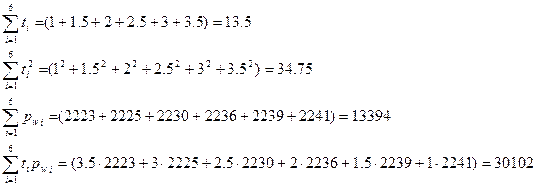
Получаем систему 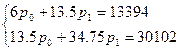, решая которую методом Гаусса получаем .

Следовательно, функция, аппроксимирующая заданную табличную функцию , имеет вид: .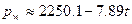

Задача 1.

Известно, что использование кислот соляной и кремнефтористоводородной , благодаря растворению терригенных коллекторов, углубляет и развивает сеть каналов. Но одновременно и ограничивает приток пластовых вод к скважине за счет закупорки фильтрационных каналов в водоносном пласте осадками кремнефторидов.

Проблемы поиска оптимального режима обработки призабойной зоны с целью снижения пластовых потерь нефти приводят к необходимости исследования зависимости количества выпадающего осадка от свойств пластовой воды.

В таблице приведены результаты эксперимента по смешиванию 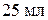пластовой воды при температуре 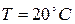с кремнефтористоводородной кислотой с последующей фильтрацией полученного раствора [1].

Таблица 13

плотность пласт, воды,	1,05	1,12	1,13	1,14	1,15	1,16	1,17
содержание осадка, % (весовое)	8,4	14,2	14,4	15,4	19,7	20,6	22,6

Получите линейную и квадратичную зависимости и постройте графики исходных данных и полученных функций

Дата добавления: 2014-01-04