Обратного преобразования Лапласа

После решения уравнений для изображений искомых величин, производимых алгебраическим путем, необходимо перейти к оригиналам функции, то есть из s-области перейти в t-область.

Из теории функции комплексного переменного известно, что если функция F (s) аналитическая в полуплоскости 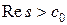стремится к 0 при 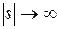в любой полуплоскости 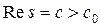равномерно относительно аргумента s, и интеграл 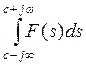абсолютно сходится, то F (s) является изображением функции:

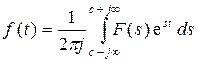. (7.3.10)

Эта формула носит название обратного преобразования Лапласа и представляет решение уравнения (7.3.1) относительно функции f (t). При этом уравнение (7.3.10) записывается в виде

.

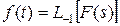На практике при переходе от изображений к оригиналам возможны два подхода:

1. Используют таблицу соответствия между функциями оператора s и функциями времени, полученную в результате расчетов по выражению (7.3.10).

Оригинал	Изображение
	1/ s
t	1/ s ^2

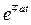
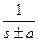
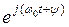
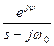
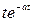
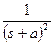
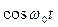
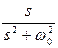
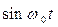
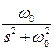
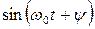
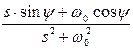
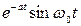
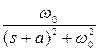
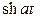
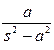
и т.д. (всего 1518 формул).

2. Применяют формулы разложения, полученные на основании теоремы разложения, справедливой при условии, что изображение функции задано в виде правильной дроби

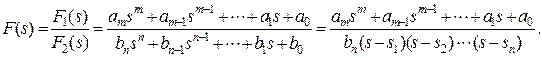(7.3.11)

Для всех физически реализуемых цепей m ≤ n, а_k и b_k -вещественные числа, s ₁, s ₂, ... s_n - корни уравнения

F ₂(s) = 0. (7.3.12)

В зависимости то того, какие корни будут получены в результате решения уравнения (7.3.12), возможны следующие случаи:

а) Корни различные (нулевых и кратных корней нет), вещественные и отрицательные.

В этом случае формула разложения будет иметь вид

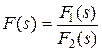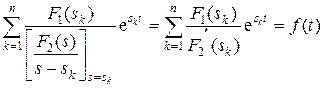≓ . (7.3.13)

б) Нулевой корень, то есть имеется наряду с простыми различными корнями один корень равный нулю, то есть 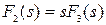, тогда формула разложения примет вид

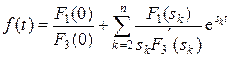. (7.3.14)

в) Комплексно сопряженные корни уравнения F ₂(s) = 0 s_k и s_k ^* - при вычислении соответствующих им слагаемых, стоящих в правой части уравнений (7.3.13) или (7.3.14), достаточно определить слагаемое для одного из этих корней, например s_k, а для сопряженного корня s_k^* следуетвзять сопряженное значение этого слагаемого. Сумма, соответствующая этим двум слагаемым, равна удвоенному значению действительной части, найденной для одного из корней

.

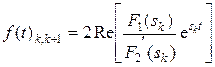в) Корни кратные - если в уравнении (7.3.14) F ₂(s) = 0 имеет q различных корней (s ₁, s ₂ … s_q) и из них корень s ₁ кратностью m ₁, корень s ₂ кратностью m ₂, корень s_q кратностью m_q, то по изображению 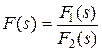оригинал f (t) вычисляется по формуле

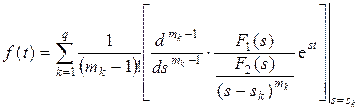. (7.3.15)

Здесь выражение, стоящее в знаменателе 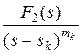, надо сначала сократить на 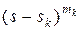и лишь после этого дифференцировать.

Если уравнение 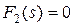содержит одновременно и простые и кратные корни, то для определения слагаемых, соответствующих простым корням, используется формулы (7.3.13) или (7.3.24) (если имеется один простой корень равный 0), а для кратных - формула (7.3.15).

В уравнениях (7.3.13) и (7.3.14) число слагаемых под знаком равно числу корней уравнения 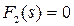, причем коэффициенты при 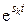можно сопоставить с постоянными интегрирования дифференциальных уравнений цепи в классическом методе расчета.

Дата добавления: 2014-01-04