Формула Хартли

Количество информации

При изучении различных явлений и объектов окружающего мира люди стремились связать с этими объектами число, ввести их количественную меру. Люди научились измерять расстояния, взвешивать различные предметы, вычислять площади фигур и объёмы тел. Научившись измерять время, его длительность, мы до сих пор пытаемся понять его природу. Термометр был придуман за много лет до того, как учёные поняли, что он измеряет: с момента появления первого термометра до создания термодинамики прошло примерно три столетия. Количественное изучение некоторого явления, объекта может опережать его качественное изучение, процесс формирования соответствующего понятия может следовать за количественным изучением.

Похожая ситуация сложилась и в отношении информации. Р. Хартли в 1928, а затем К. Шеннон в 1948 предложили формулы для вычисления количества информации, однако на вопрос о том, что такое информация, они так и не ответили.

В теории связи информация выступает в виде различных сообщений: например, букв или цифр, как в телеграфии, или в виде непрерывной функции времени, как при телефонии или радиовещании.

В любом из указанных примеров, в конечном итоге, задача состоит в передаче смыслового содержания человеческой речи.

В свою очередь, человеческая речь может быть представлена в звуковых колебаниях или в письменном изложении.

Это ещё одно из свойств этого вида информации: способность представлять одно и то же смысловое содержание в различном физическом виде.

Впервые на это обратил особое внимание У. Эшби.

Представление информации в различном физическом виде называется кодированием. Для того, чтобы общаться с другими людьми, человеку приходится постоянно заниматься кодированием, перекодированием и декодированием. Очевидно, что по каналам связи информация может передаваться в самых различных системах кодирования.

Р. Хартли первым ввел в теорию передачи информации методологию «измерения количества информации». При этом Р. Хартли считал, что информация, которую он собирался измерять, это «… группа физических символов – слов, точек, тире и т. п., имеющих по общему соглашению известный смысл для корреспондирующих сторон». Таким образом, Хартли ставил перед собой задачу ввести какую-то меру для измерения кодированной информации.

Пусть передаётся последовательность из n символов а₁а₂а₃…а_n, каждый из которых принадлежит алфавиту А_m, содержащему m символов. Чему равно число К различных вариантов таких последовательностей?

Если n = 1 (передаётся один символ), то K = m; если n=2 (передаётся последовательность из 2-х символов), то K = m*m = m²; в общем случае для последовательности из n символов получим

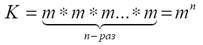
Количество информации, содержащееся в такой последовательности, Хартли предложил вычислять как логарифм числа K по основанию 2:

I = Log₂ K,

где K = mⁿ.

То есть, количество информации, содержащееся в последовательности из n символов из алфавита A_m, в соответствии с формулой Хартли равно

I = Log₂(mⁿ) = n Log₂m

Замечание 1. Хартли предполагал, что все символы алфавита A_m могут с равной вероятностью (частотой) встретиться в любом месте сообщения. Это условие нарушается для алфавитов естественных языков: например, не все буквы русского алфавита встречаются в тексте с одинаковой частотой.

Замечание 2. Любое сообщение длины n в алфавите A_m будет содержать одинаковое количество информации. Например, в алфавите {0; 1} сообщения 00111, 11001 и 10101 содержат одинаковое количество информации. Это означает, что при вычислении количества информации, содержащегося в сообщении, мы отвлекаемся от его смыслового содержания. «Осмысленное» сообщение и сообщение, полученное из него произвольной перестановкой символов, будут содержать одинаковое количество информации.

Пример. В телеграфном сообщении используются два символа – точка (.) и тире (-), т.е. алфавит состоит из m = 2 символов. Тогда при передаче одного символа (n =1) количество информации I = Log₂2 = 1. Это количество было принято за единицу измерения количества информации и называется 1 бит (от английского binary unit = bit). Если телеграфное сообщение в алфавите {.; -} содержит n символов, то количество информации I = n Log₂2 = n (бит).

С помощью символов 0 и 1 кодируется информация в компьютере и при передаче в вычислительных сетях, т.е. алфавит состоит из двух символов {0; 1}; один символ и в этом случае содержит I = Log₂2 = 1 бит информации, поэтому сообщение длиной n символов в алфавите {0; 1} в соответствии с формулой Хартли I = n Log₂m (I = n Log₂2 = n) будет содержать n бит информации.

Если рассматривать передачу сообщений в алфавите русского языка, состоящего из 33 букв, то количество информации, содержащееся в сообщении из n символов, вычисленное по формуле Хартли, равно

I = n*Log₂33 ≈ n* 5.0444 бит.

Английский алфавит содержит 26 букв, один символ содержит

Log₂ 26 ≈4.7 бит,

поэтому сообщение из n символов, вычисленное по формуле Хартли, содержит n* Log₂ 26 ≈ 4.7 *n бит информации.

Однако, этот результат не является правильным, так как не все буквы встречаются в тексте с одинаковой частотой. Кроме того, к буквам алфавита надо добавить разделительные знаки: пробел, точку, запятую и др.

Формула I = Log2 K внешне напоминает формулу Больцмана для вычисления энтропии системы с N равновероятными микросостояниями:

S= - k*Ln(W),

где k - постоянная Больцмана = 1,38*10^-23, а W - вероятность спонтанного принятия одного из микросостояний системы в единицу времени t = 10^-13 сек., W = 1/N, т.е.

S= -k*Ln(1/N) = k*Ln(N),

что полностью согласуется с формулой S= - k*Ln(W) за исключением множителя k и основания логарифма. Из-за этого внешнего сходства величину Log₂K в теории информации также называют энтропией и обозначают символом H.

Информационная энтропия – это мера неопределённости состояния некоторой случайной величины (физической системы) с конечным или счётным числом состояний.

Случайная величина ( с.в. ) – это величина, которая в результате эксперимента или наблюдения принимает числовое значение, заранее неизвестно какое.

Итак, пусть X – случайная величина, которая может принимать N различных значений x₁, x₂, … x_N; если все значения с.в. X равновероятны, то энтропия (мера неопределённости) величины X равна:

H(X) = Log₂ N.

Замечание. Если случайная величина (система) может находиться только в одном состоянии (N=1), то её энтропия равна 0. Фактически это уже не случайная величина. Неопределённость системы тем выше, чем больше число её возможных равновероятных состояний.

Энтропия и количество информации измеряются в одних и тех же единицах – в битах.

Определение. 1 бит – это энтропия системы с двумя равновероятными состояниями.

Пусть система X может находиться в двух состояниях x1 и x2 с равной вероятностью, т.е. N = 2; тогда её энтропия H(X) = Log₂ 2 = 1 бит.

Пример такой системы даёт нам монета, при подбрасывании которой выпадает либо орёл (x1), либо решка (x2). Если монета «правильная», то вероятность выпадения орла или решки одинаковая и равна 1/2.

Дадим ещё одно определение единицы измерения информации.

Определение. Ответ на вопрос любой природы (любого характера) содержит 1 бит информации, если он с равной вероятностью может быть «да» или «нет».

Пример. Игра в «пусто-густо». Вы прячете мелкий предмет в одной руке и предлагаете партнёру угадать, в какой руке вы его спрятали. Он спрашивает вас «в левой руке?» (или просто выбирает руку: левую или правую). Вы отвечаете «да», если он угадал, или «нет», в противном случае. При любом варианте ответа партнёр получает 1 бит информации, а неопределённость ситуации полностью снимается.

Формулу Хартли можно использовать при решении задач на определение выделенного элемента некоторого заданного множества. Этот результат можно сформулировать в виде следующего правила:

если в заданном множестве M, состоящем из N элементов, выделен некоторый элемент x, о котором ничего более неизвестно, то для определения этого элемента необходимо получить Log₂N бит информации.

Рассмотрим несколько задач на применение формулы Хартли.

Задача 1. Некто задумал натуральное число в диапазоне от 1 до 32. Какое минимальное число вопросов надо задать, чтобы гарантированно угадать задуманное (выделенное) число. Ответы могут быть только «да» или «нет».

Комментарий. Можно попытаться угадать задуманное число простым перебором. Если повезёт, то придётся задать только один вопрос, а при самом неудачном варианте перебора придётся задать 31 вопрос. В предложенной задаче нужно определить минимальное число вопросов, с помощью которых вы гарантированно определяете задуманное число.

Решение. По формуле Хартли можно вычислить количество информации, которое необходимо получить для определения выделенного элемента x из множества целых чисел {1,2,3 ……, 32}. Для этого необходимо получить Н = Log₂ 32 = 5 бит информации. Вопросы надо задавать так, чтобы ответы на них были равновероятны. Тогда ответ на каждый такой вопрос будет приносить 1 бит информации. Например, можно разбить числа на две равные группы от 1 до 16 и от 17 до 32 и спросить, в какой группе находится задуманное число. Далее, аналогично следует поступить с выделенной группой, которая содержит уже лишь 16 чисел, и т.д. Пусть, например, задумано число 7.

Вопрос №1: Задуманное число принадлежит множеству {17.. 32}? Ответ «нет» приносит вам 1 бит информации. Мы теперь знаем, что число принадлежит множеству {1.. 16}.

Вопрос №2: Задуманное число принадлежит множеству {1.. 8}? Ответ «да» приносит вам ещё 1 бит информации. Мы теперь знаем, что число принадлежит множеству {1.. 8}.

Вопрос №3: Задуманное число принадлежит множеству {1.. 4}? Ответ «нет» приносит вам ещё 1 бит информации. Мы теперь знаем, что число принадлежит множеству {5.. 8}.

Вопрос №4: Задуманное число принадлежит множеству {7; 8}? Ответ «да» приносит вам ещё 1 бит информации. Мы теперь знаем, что число принадлежит множеству {7; 8}.

Вопрос №5: Задуманное число равно 8? Ответ «нет» приносит вам ещё 1 бит информации. Мы теперь знаем, что задуманное число равно 7. Задача решена. Было задано пять вопросов, в ответ получено 5 бит информации и определено задуманное число.

Задача 2. (Задача о фальшивой монете). Имеется 27 монет, из которых 26 настоящих и одна фальшивая. Каково минимальное число взвешиваний на рычажных весах, за которое можно гарантированно определить одну фальшивую монету из 27, используя то, что фальшивая монета легче настоящей.

Рычажные весы имеют две чашки и с их помощью можно лишь установить, одинаково ли по весу содержимое чашек, и если нет, то содержимое какой из чашек тяжелее.

Решение. Это задача на определение одного выделенного элемента из 27. По формуле Хартли мы сразу можем определить количество информации, которое нужно получить для определения фальшивой монеты: оно равно I = Log₂27 = Log₂(3³) = 3 Log₂3 бит. Отметим, что ещё не зная стратегии взвешивания, можно сказать, сколько информации мы должны получить для решения задачи.

Если положить на чашки весов равное количество монет, то возможны три равновероятных исхода:

1. левая чашка тяжелее правой (Л > П);

2. левая чашка легче правой (Л < П);

3. левая чашка находится в равновесии с правой (Л = П);

Система «рычажные весы» может находиться в трёх равновероятных состояниях, поэтому одно взвешивание даёт Log₂3 бит информации. Всего для решения задачи надо получить I = 3 Log₂3 бит информации, значит надо сделать три взвешивания для определения фальшивой монеты. Мы уже знаем минимальное число взвешиваний, но ещё не знаем, как их следует проводить. Стратегия должна быть такой, чтобы каждое взвешивание давало максимальное количество информации. Разделим все монеты на три равные кучки A, B и C по 9 штук в каждой. Фальшивая монета, обозначим её буквой f, может с равной вероятностью находиться в любой из трёх кучек. Выберем любые две из них, например А и В, и взвесим их. Возможны три исхода:

1) А тяжелее В (А > В); значит f ÎВ;

2) А легче В (А < В); значит f ÎА;

3) А находится в равновесии с В (А = В); значит f ÎС.

При любом исходе мы определим в какой кучке находится фальшивая монета f, но в этой кучке будет уже только 9 монет. Разобъём её на три равные кучки Al, Bl, С1 по 3 монеты в каждой. Выберем любые две и взвесим их. Как и на предыдущем шаге, мы определим ту кучку монет, в которой находится фальшивая монета, но теперь кучка состоит только из трёх монет. Выберем любые две монеты и взвесим их. Это будет последнее, третье взвешивание, после которого мы найдём фальшивую монету.

Задача 3. Не используя калькулятор, оцените с точностью до одного бита энтропию системы, которая может с равной вероятностью находится в 50 состояниях.

Решение. По формуле Хартли Н = Log₂50. Оценим данное выражение.

Очевидно, 32 < 50 < 64; логарифмируем это неравенство -> Log232 < Log250 < Log264 -> 5 < Log250 < 6. Энтропия системы с точностью до 1 бита 5 < Н < 6.

Задача 4. Известно, что энтропия системы составляет 7 бит. Определите число состояний этой системы, если известно, что все они равновероятны.

Решение. Обозначим через N число состояний системы. Так как все состояния равновероятны, то Н = Log₂N -> N = 2^Н, т.е. N = 2⁷ = 128.30.

Дата добавления: 2014-01-04